单选题 (共 29 题 ),每题只有一个选项正确
$\left(\frac{4}{2^{\sqrt{2}}}\right)^{2+\sqrt{2}}$ 的值为
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
$\text{E.}$ 4
$\lim _{x \rightarrow \infty} \frac{\sqrt{x^2-2}+3 x}{x+5}$ 的值为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\text{E.}$ 5
在公比为正数的等比数列 $\left\{a_n\right\}$ 中, $a_2+a_4=30 ,a_4+a_6=\frac{15}{2}$, 则 $a_1$ 的值为
$\text{A.}$ 48
$\text{B.}$ 56
$\text{C.}$ 64
$\text{D.}$ 72
$\text{E.}$ 80
$f(x)$ 为多项式函数, $g(x)=x^2 f(x)$,若 $f(2)=1, f^{\prime}(2)=3$, 则 $g^{\prime}(2)$ 的值为
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 16
$\text{D.}$ 18
$\text{E.}$ 20
已知 $\tan \theta < 0 , \cos \left(\frac{\pi}{2}+\theta\right)=\frac{\sqrt{5}}{5}$, 求 $\cos \theta$ 的值为
$\text{A.}$ $-\frac{2 \sqrt{5}}{5}$
$\text{B.}$ $-\frac{\sqrt{5}}{5}$
$\text{C.}$ 0
$\text{D.}$ $\frac{\sqrt{5}}{5}$
$\text{E.}$ $\frac{2 \sqrt{5}}{5}$
已知函数 $f(x)=2 x^3-9 x^2+a x+5$ 在 $x=1$ 处取得极大值, 在 $x=b$ 处取得极小值,则 $a+b$ 的值为
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 16
$\text{D.}$ 18
$\text{E.}$ 20
等差数列$a_n$的各项均为正数,首项与公差相等, $\sum_{k=1}^{15} \dfrac{1}{\sqrt{a_k}+\sqrt{n_{k+1}}}=2$, 则 $a_4$的值
$\text{A.}$ 6
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 9
$\text{E.}$ 10
过点 $(0.4)$ 作曲线 $y=x^3-x+2$ 的切线, 则这切线在 $x$ 轴上的截距为
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $-1$
$\text{C.}$ $-\frac{3}{2}$
$\text{D.}$ $-2$
$\text{E.}$ $-\frac{5}{2}$
函数 $f(x)=a-\sqrt{3} \tan 2 x$ 在闭区间 $\left[-\frac{\pi}{6}, b\right]$ 上的最大值为7,最小值为 3 , 则 $a \times b$ 的值为
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{5 \pi}{12}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{\pi}{4}$
$\text{E.}$ $\frac{\pi}{6}$
记曲线 $y=x^3+x^2, y=-x^2+k(4 < k < 5)$ 与 $y$ 轴围成的面积为$A$,这两条曲线与直线 $x=2$围成的面积为$B$,如图所示, $A=B$. 则 $k$ 的值为
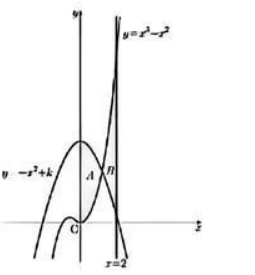
$\text{A.}$ $\frac{25}{6}$
$\text{B.}$ $\frac{13}{3}$
$\text{C.}$ $\frac{9}{2}$
$\text{D.}$ $\frac{14}{3}$
$\text{E.}$ $\frac{29}{6}$
如图所示,四边形 $A B C D$ 内接于圆, $\overline{A B}=5, \overline{A C}=3 \sqrt{5}, \overline{A D}=7$, $\angle B A C=\angle C A D$. 则圆的半径为
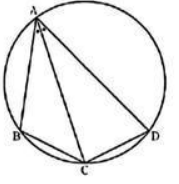
$\text{A.}$ $\frac{5 \sqrt{2}}{2}$
$\text{B.}$ $\frac{8 \sqrt{2}}{5}$
$\text{C.}$ $\frac{5 \sqrt{2}}{3}$
$\text{D.}$ $\frac{8 \sqrt{2}}{3}$
$\text{E.}$ $\frac{9 \sqrt{2}}{4}$
定义在全体实数上的连续函数 $f(x)$ 满足下列条件:
当 $n-1 < x < n$ 时, $|f(x)|=|6(x-n+1)(x-n)|(n$ 为正整数 $)$ $\int_{\frac{1}{2}}^4 f(x) \mathrm{d} x$ 的值为
定义在开区间$(0,4)$上的函数 $ g(x)=\int_0^x f(t) \mathrm{d} t-\int_x^4 f(t) \mathrm{d} t $ 若$g(x)$在 $x=2$ 处取得最小值,则 $\int_{\frac{1}{2}}^4 f(x) \mathrm{d} x$ 的值为
$\text{A.}$ $-\frac{3}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{3}{2}$
$\text{E.}$ $\frac{5}{2}$
对于正整数$m(m \ge 2)$,使得 $m^{12}$的$n$次方根为整数的正整数$n(n \ge2)$的个数记为$f(m)$,则 $\sum_{m=2}^9 f(m)$ 的值为
$\text{A.}$ 37
$\text{B.}$ 42
$\text{C.}$ 47
$\text{D.}$ 52
$\text{E.}$ 57
$f(x)$ 为多项式函数, $g(x)$ 定义如下
$$
g(x)=\left\{\begin{array}{cc}
x & (x < -1 \text { 或 } x>1) \\
f(x) & (-1 \leq x \leq 1)
\end{array}\right.
$$
关于函数 $h(x)=\lim _{t \rightarrow 0^{+}} g(x+t) \times \lim _{t \rightarrow 2^{+}} g(x+t)$ 下下列说法正确的是
甲. $h(1)=3$
乙. $h(x)$ 在全体实数上连续
丙.若$g(x)$在区间$[-1,1]$上单调递减,且$g(-1)=-2$,则$h(x)$在全体实数上具有最小值
$\text{A.}$ 甲
$\text{B.}$ 乙
$\text{C.}$ 甲乙
$\text{D.}$ 甲丙
$\text{E.}$ 乙丙
在各项均为正整数,且满足下列条件的数量$a_n$中,$a_9$可能的最大值和最小值分别是$M$和$m$, 则$M+m$的值为
① $a_7=40$
② 对于任意正整数$n$,
$$
a_{n+2}= \begin{cases}a_{n+1}+a_n & \left(a_{n+1} \text { 不是3的倍数 }\right) \\ \frac{1}{3} a_{n+1} & \left(a_{n+1} \text { 是3的倍数 }\right)\end{cases}
$$
$\text{A.}$ 216
$\text{B.}$ 218
$\text{C.}$ 220
$\text{D.}$ 222
$\text{E.}$ 224
$\left(x^3+3\right)^5$ 的展开开式中, $x^9$ 项的系数为
$\text{A.}$ 30
$\text{B.}$ 60
$\text{C.}$ 90
$\text{D.}$ 120
$\text{E.}$ 150
从数字1,2,3,4,5可重复地选4个,能排列成多少大于4000的奇数
$\text{A.}$ 125
$\text{B.}$ 150
$\text{C.}$ 175
$\text{D.}$ 200
$\text{E.}$ 225
盒子中装有5个白色口罩和9个黑色口罩,一次性从盒中随机抽取3个,至少一个白色口罩的概率
$\text{A.}$ $\frac{8}{13}$
$\text{B.}$ $\frac{17}{26}$
$\text{C.}$ $\frac{9}{13}$
$\text{D.}$ $\frac{19}{26}$
$\text{E.}$ $\frac{10}{13}$
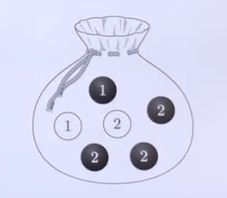
袋中装有6个小球,其中2个白色,写有数字1和2. 4个黑色,1个写有数字1,3个写有数字2.
一次性从袋中随机取出3个球,记“取出的是1个白球,2个黑球”为事件A,“3个球上数字的乘积为8”为事件B,则 $P(A \cup B)$为
$\text{A.}$ $\frac{11}{20}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{13}{20}$
$\text{D.}$ $\frac{7}{10}$
$\text{E.}$ $\frac{3}{4}$
某公司生产的洗发水,每瓶容量服从$N(m, \sigma ^2)$ 的正态分布,随机抽取16瓶,用均值推断m的95%置信区间为 $746.1 \le m \le 755.9$ 若随机抽取n瓶,用样本均值推断m的99%置信区间为$a \leqslant m \leqslant b$. 已知 $P(|Z| \leqslant 1.96)=0.95, P(|Z| \leqslant 2.58)=0.99$, 要使 $b-a$ 不大于 $6 . n$ 最小为
$\text{A.}$ 70
$\text{B.}$ 74
$\text{C.}$ 78
$\text{D.}$ 82
$\text{E.}$ 86
连续型随机变量X的取值为 $0 \le X \le a$, X的概率密度如下图

若 $P(X \le b)-P(X \geqslant b)=\frac{1}{4}, P(X \le \sqrt{5})=\frac{1}{2}$, 则 $a+b+c$ 的值为
$\text{A.}$ $\frac{11}{2}$
$\text{B.}$ 6
$\text{C.}$ $\frac{13}{2}$
$\text{D.}$ 7
$\text{E.}$ $\frac{15}{2}$
$\lim _{x \rightarrow 0} \frac{\ln (x+1)}{\sqrt{x+4}-2}$ 的值为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\text{E.}$ 5
$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{k=1}^n \sqrt{1+\frac{3 k}{n}}$ 的值为
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{13}{9}$
$\text{C.}$ $\frac{14}{9}$
$\text{D.}$ $\frac{5}{3}$
$\text{E.}$ $\frac{16}{9}$
等比数列$a_n$满足 $ \lim _{n \rightarrow \infty} \frac{a_n+1}{3^n+2^{2 n-1}}=3 $ 则 $a_2$值为
$\text{A.}$ 16
$\text{B.}$ 18
$\text{C.}$ 20
$\text{D.}$ 22
$\text{E.}$ 24
如图所示, 某三维形体的底面由曲线 $ y=\sqrt{\sec ^2 x+\tan x}\left(0 \leqslant x \leqslant \frac{\pi}{3}\right) $ 与 x 轴、 y 轴和 $ x=\frac{\pi}{3} $ 围成. 用垂直x轴的平面截该形体得到的节面均为正方形,则该形体的体积是
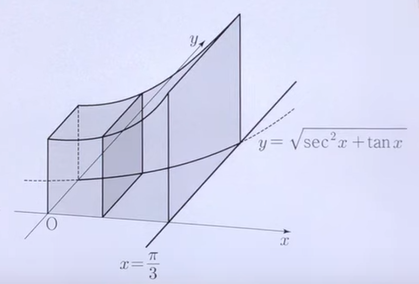
$\text{A.}$ $\frac{\sqrt{3}}{2}+\frac{\ln 2}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}+\ln 2$
$\text{C.}$ $ \sqrt{3}+\frac{\ln 2}{2} $
$\text{D.}$ $\sqrt{3}+\ln 2$
$\text{E.}$ $\sqrt{3}+2 \ln 2$
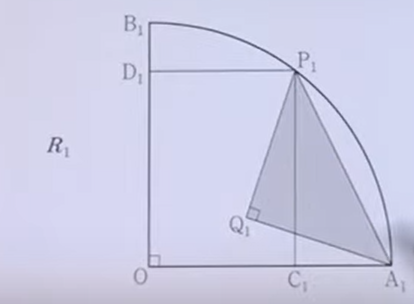
如图所示,有圆心为$O$,半径为$1$,圆心角为$\frac{\pi}{2}$的扇形 $OA_1B_1$, 弧$A_1B_1$ 上有一点$P_1$,到$OA_1$的垂直为$C_1$,到$OB_1$的垂足为$D_1$,矩形$OC_1P_1D_1$满足 $\overline{O C_1}: \overline{O D_1}=3: 4$ 扇形$OA_1B_1$内部的点$Q_1$满足 $\overline{P_1 Q_1}=\overline{A_1 Q_1}, \angle P_1 Q_1 A_1=\frac{\pi}{2},$ 将等腰直角三角形 $P_1Q_1A_1$涂上阴影,得到图像$R_1$,在图像$R_1$的基础上,在$OA_1$上取点$A_2$, $OB_1$上取点$B_2$,使 $\overline{O Q_1}=\overline{OA_2} =\overline{OB_2} $ 以O为圆心, $\overline{O Q_1} $ 为半径,做圆心为 $\frac {\pi} {2}$ 扇形 $OA_2B_2$, 与$R_1$类似的方法做出 $P_2, C_2,D_2,Q_2$,并得到图像$R_2$, 重复这一过程n次,得到图像${R_n}$ 阴影部分的面积合计为 $S_n$,
求 $\lim_{n \rightarrow\infty}S_n$
$\text{A.}$ $\frac{9}{40}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{11}{40}$
$\text{D.}$ $\frac{3}{10}$
$\text{E.}$ $\frac{13}{40}$
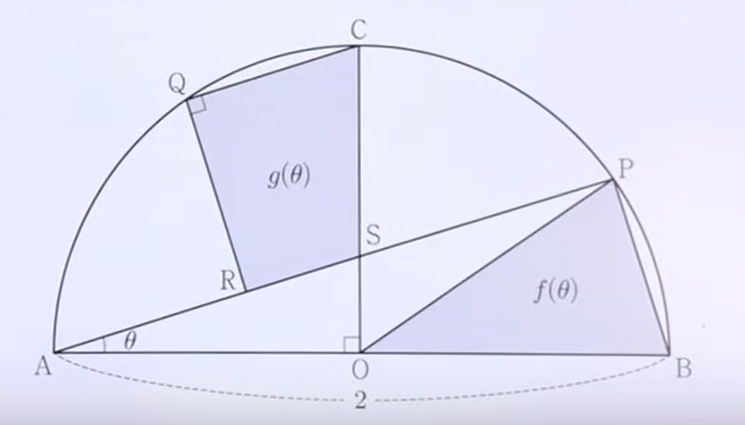
如图,$\angle \mathrm{AOC}=\frac{\pi}{2}$, 弧上有$P,Q$两点,且 $\overline{\mathrm{PB}}=\overline{\mathrm{QC}}$, 在线段$\mathrm{AP}$上画一个点$\mathrm{R}$使得$\angle \mathrm{CQR}=\frac{\pi} {2}$ ,
设$\mathrm{S}$ 为线段 $\mathrm{AP}$ 和线段 $\mathrm{CO}$ 的交点。 当$\angle \mathrm{PAB}=\theta$时,三角形$\mathrm{POB}$的面积为$f(\theta)$,矩形$\mathrm{CQRS}$的面积为$g(\theta)$。
求 $\lim \frac{3 f(\theta)-2 g(\theta)}{\theta^2}$ 的值是多少? (其中$0 < \theta < \frac{\pi}{4}$)
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\text{E.}$ 5
坐标空间中的点$\mathrm{A}(2,2,-1)$ 设$\mathrm{B}$为关于轴$x$对称的点。 直线 $\mathrm{BC}$ 相对于点 $\mathrm{C}(-2,1,1)$ 的长度是多少?
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\text{E.}$ 5
一条焦点为 $\mathrm{F}\left(\frac{1}{3}, 0\right)$ 且准线 $x=-\frac{1}{3}$ 的抛物线经过点 $(a , 2)$,$a$的值是多少?
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
$\text{E.}$ 5
填空题 (共 4 题 ),请把答案直接填写在答题纸上
求满足方程 $\log _2(3 x+2)=2+\log _2(x-2)$ 的 $x$ 值
对于函数 $f(x)$, 已知 $f^{\prime}(x)=4 x^3-2 x$, 且 $f(0)=3$, 求 $f(2)$ 的值
数列 $ \left\{a_n\right\},\left\{b_n\right\} $ 满足
$$
\sum_{k=1}^5\left(3 a_k+5\right)=55, \quad \sum_{k=1}^5\left(a_k+b_k\right)=32
$$ ,
求 $ \sum_{k=1}^5 b_k $ 的值
求使方程 $2 x^3-6 x^2+k=0$ 恰有 2 个互异实数解的整数 $k$ 共有多少个
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
点 $P$ 在直线上运动, $t(t \geqslant 0)$ 时刻的速度 $v(t)$ 和加速度 $a(t)$ 满足以下条件,
(1) 当 $0 \leqslant t \leqslant 2$ 时, $r(t)=2 t^3-8 t$.
(2) 当 $t \geqslant 2$ 时, $a(t)=6 t+4$.
求点 $P$ 从 $t=0$ 到 $t=3$ 时刻移动的距离
对于正整数 $n$, 函数$f(x)$ 定义如下:
$$
f(x)=\left\{\begin{array}{cc}
\left|3^{x+2}-n\right| & (x < 0) \\
\left|\log _2(x+4)-n\right| & (x \geqslant 0)
\end{array}\right.
$$
对于实数 $t$, 记方程 $f(x)=t$ 的不同实数解的数量为 $g(t)$. 求使得函数 $g(t)$ 的最大值为 4 的所在正 整数 $n$ 的和
最高次项系数为1的三次函数$f(x)$和实数域上的连续函数$g(x)$满足下列条件,求$f(4)$
(1) 对于任意实数 $x, f(x)=f(1)+(x-1) f^{\prime}(g(x))$.
(2) 函数 $g(x)$ 的最小值为 $\frac{5}{2}$.
(3) $f(0)=-3, f(g(1))=6$.
有6张卡片,正面分别写有数字1-6,背面都写有数字0,起初将这些卡片正面朝上排成一排,且第k个位置上的卡片恰写有数字k,下面利用这6张卡片和一枚均匀的骰子进行如下实验:
掷出骰子,若点数为k,则将第k个位置上的卡片翻面,放在原处。
进行上述实验3次,若卡片朝上的数字之和为偶数,在这一条件下,骰子恰有一次点数为1的概率为$\dfrac{q}{p}$,求$p+q$的值(p,q互为质数)
集合$X=\{ x | x是不大于10的正整数 \}$ 求满足下列条件的函数 $f:X \to X$ 共有多少个
(l) 对于任意不大于9的正整数 $x$, 有 $f(x) \leqslant f(x+1)$.
(2) 当 $1 \leqslant x \leqslant 5$ 时, $f(x) < x$ , 当 $6 \leqslant x \leqslant 10$ 时 $f(x) \geqslant x$.
(3) $f(6)=f(5)+6$.
对于常数$a、b、c$,函数$f(x)=a c^{2 x}+b e^2+c$满足以下条件率:
(a) $\lim _{x \rightarrow-\infty=} \frac{f(x)+6}{e^x}=1$
(b) $f(\ln 2)=0$
如果 $g(x)$ 是函数 $f(x)$ 的指数,且 $\int_0^{14} g(x) d x=p+q \ln 2$。 找出 $p+q$ 的值。
(其中,$p和q$是有理数,$\ln 2$是无理数。)
对于最高阶项系数为正的三次函数$f(x)$和函数$g(x)=e^{\sin\pi x}-1$,复合函数$h (x)=g(f(x))$ 满足条件
(A) 函数 $h(x)$ 在 $x=0$ 时的最大值为 0。
(B) 方程$h(x)=1$在开区间$(0,3)$内的不同实根个数为7。
当 $f(3)=\frac{1}{2}$ 且 $f^{\prime}(3)=0$ 时,$f(2)=\frac{q}{p}$。 找出 $p+q$ 的值。 (其中,$p$ 和 $q$ 是互质自然数。)