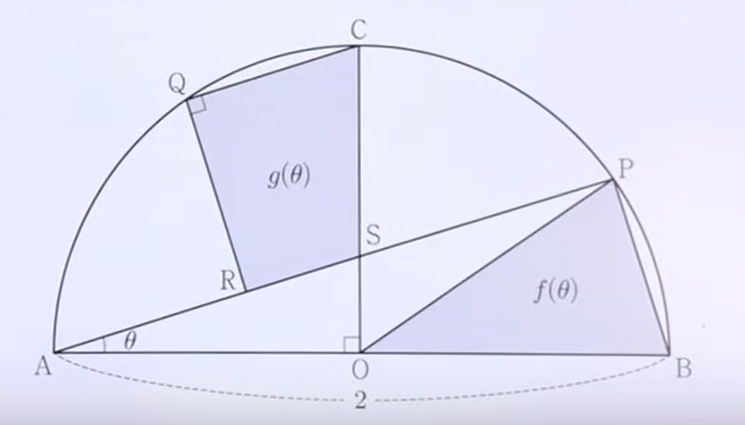
如图,$\angle \mathrm{AOC}=\frac{\pi}{2}$, 弧上有$P,Q$两点,且 $\overline{\mathrm{PB}}=\overline{\mathrm{QC}}$, 在线段$\mathrm{AP}$上画一个点$\mathrm{R}$使得$\angle \mathrm{CQR}=\frac{\pi} {2}$ ,
设$\mathrm{S}$ 为线段 $\mathrm{AP}$ 和线段 $\mathrm{CO}$ 的交点。 当$\angle \mathrm{PAB}=\theta$时,三角形$\mathrm{POB}$的面积为$f(\theta)$,矩形$\mathrm{CQRS}$的面积为$g(\theta)$。
求 $\lim \frac{3 f(\theta)-2 g(\theta)}{\theta^2}$ 的值是多少? (其中$0 < \theta < \frac{\pi}{4}$)
设$\mathrm{S}$ 为线段 $\mathrm{AP}$ 和线段 $\mathrm{CO}$ 的交点。 当$\angle \mathrm{PAB}=\theta$时,三角形$\mathrm{POB}$的面积为$f(\theta)$,矩形$\mathrm{CQRS}$的面积为$g(\theta)$。
求 $\lim \frac{3 f(\theta)-2 g(\theta)}{\theta^2}$ 的值是多少? (其中$0 < \theta < \frac{\pi}{4}$)

A. 1
B. 2
C. 3
D. 4
D. 5