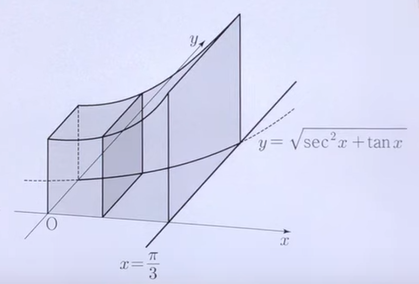
如图所示, 某三维形体的底面由曲线 $ y=\sqrt{\sec ^2 x+\tan x}\left(0 \leqslant x \leqslant \frac{\pi}{3}\right) $ 与 x 轴、 y 轴和 $ x=\frac{\pi}{3} $ 围成. 用垂直x轴的平面截该形体得到的节面均为正方形,则该形体的体积是

A. $\frac{\sqrt{3}}{2}+\frac{\ln 2}{2}$
B. $\frac{\sqrt{3}}{2}+\ln 2$
C. $ \sqrt{3}+\frac{\ln 2}{2} $
D. $\sqrt{3}+\ln 2$
D. $\sqrt{3}+2 \ln 2$