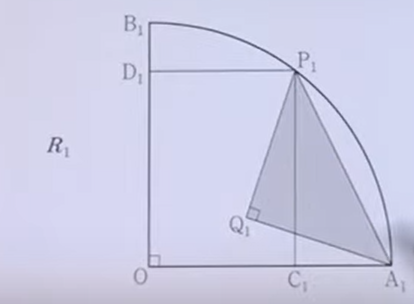
如图所示,有圆心为$O$,半径为$1$,圆心角为$\frac{\pi}{2}$的扇形 $OA_1B_1$, 弧$A_1B_1$ 上有一点$P_1$,到$OA_1$的垂直为$C_1$,到$OB_1$的垂足为$D_1$,矩形$OC_1P_1D_1$满足 $\overline{O C_1}: \overline{O D_1}=3: 4$ 扇形$OA_1B_1$内部的点$Q_1$满足 $\overline{P_1 Q_1}=\overline{A_1 Q_1}, \angle P_1 Q_1 A_1=\frac{\pi}{2},$ 将等腰直角三角形 $P_1Q_1A_1$涂上阴影,得到图像$R_1$,在图像$R_1$的基础上,在$OA_1$上取点$A_2$, $OB_1$上取点$B_2$,使 $\overline{O Q_1}=\overline{OA_2} =\overline{OB_2} $ 以O为圆心, $\overline{O Q_1} $ 为半径,做圆心为 $\frac {\pi} {2}$ 扇形 $OA_2B_2$, 与$R_1$类似的方法做出 $P_2, C_2,D_2,Q_2$,并得到图像$R_2$, 重复这一过程n次,得到图像${R_n}$ 阴影部分的面积合计为 $S_n$,
求 $\lim_{n \rightarrow\infty}S_n$
求 $\lim_{n \rightarrow\infty}S_n$

A. $\frac{9}{40}$
B. $\frac{1}{4}$
C. $\frac{11}{40}$
D. $\frac{3}{10}$
D. $\frac{13}{40}$