云南师范大学附属中学2025届高三高考适应性月考试卷数学四(公众号昭高数研基地)

导出试卷

云南师范大学附属中学2025届高三高考适应性月考试卷数学四(公众号昭高数研基地)

一、单选题（共 8 题），每题只有一个选项正确

1. 在复平面内, 复数

Z = i^{2024} + i^{2025}

, 则

\bar{Z}

的虚部为

A.

B.

-1

C.

D.

- i

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 已知

a, b

为单位向量, 且

a

在

b

上的投影向量为

\frac{1}{2} b

, 则

| a - 2 b | =

A.

B.

\sqrt{5}

C.

D.

\sqrt{3}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 已知函数

f (x) = \sin (x - 1) + x

, 若

f (a) + f (b) = 2

, 则

a + b =

A.

B.

C.

D.

-2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 在

△ A B C

中,

\tan A + \tan B + \tan A \tan B = 1

, 则

\cos C =

A.

- \frac{\sqrt{3}}{2}

B.

- \frac{\sqrt{2}}{2}

C.

\frac{\sqrt{2}}{2}

D.

\frac{\sqrt{3}}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 已知等比数列

{a_{n}}

的前

n

项和为

S_{n}

, 且

a_{n} > 0

, 若

S_{5} = 5, S_{15} = 105

, 则

S_{20} =

A.

550

B.

520

C.

450

D.

425

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 下列不等关系正确的是

A.

\ln \frac{1}{2} < 2^{\frac{1}{2}} < \sin \frac{1}{2}

B.

\sin 1 < \cos 1 < \tan 1

C.

\sqrt{8} - \sqrt{7} < \sqrt{7} - \sqrt{6} < \sqrt{6} - \sqrt{5}

D.

\log_{2} 3 < \log_{3} 4 < \log_{4} 5

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知函数

f (x) = \sin ω x + \cos ω x (ω > 0)

的图象的一条对称轴是

x = 2 π

, 且

f (x)

在

[0, \frac{π}{2}]

上恰有两个根, 则

ω

的最大值是

A.

\frac{45}{8}

B.

\frac{41}{8}

C.

\frac{37}{8}

D.

\frac{29}{8}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知椭圆

C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)

的左、右焦点分别为

F_{1}, F_{2}

, 点

P (x_{1}, y_{1})

是

C

上的一点,

△ P F_{1} F_{2}

的内切圆圆心为

Q (x_{2}, y_{2})

, 若

x_{1} = 2, x_{2} = \sqrt{3}

, 则

C

的离心率为

A.

\frac{\sqrt{3}}{2}

B.

\sqrt{3} - 1

C.

\frac{\sqrt{3}}{3}

D.

2 - \sqrt{3}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 3 题），每题有多个选项正确

9. 云南的鲜花饼不仅是一种美味的糕点, 更是一件艺术品, 它表达了人们对生活的热爱, 可以让人们在繁忙的都市生活中, 感受春天的味道. 因此, 三朵敛瑰一个饼, 深受人们的喜爱. 由于现烤鲜花饼的保质期较短, 为了提升品质, 能让顾客吃到更新鲜的饼,某商店老板统计了该商店六月份整个月的销售量, 如下表:

则对该商店的描述正确的是

A.

该商店六月份鲜花饼日销售量的第

70 %

分位数是 550

B.

该商店六月份平均每天销售鲜花饼 500 个 (同一组数据用该组区间中点值为代表)

C.

若当天准备 550 个鲜花饼,则全部售完的概率为

\frac{2}{3}

D.

若当天准备 450 个鲜花饼,则没有全部售完的概率为

\frac{2}{5}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 数列

{a_{n}}

满足

a_{n + 1} + 2 a_{n} a_{n + 1} - a_{n} = 0 (n \in N^{*}), a_{1} = 1

, 则下列结论正确的是

A.

若

b_{n} = 3^{\frac{1}{a_{n}}}

, 则

{b_{n}}

为等比数列

B.

若

c_{n} = \frac{1}{n} (\frac{1}{a_{1}} + \frac{1}{a_{2}} + \dots + \frac{1}{a_{n}})

, 则

{c_{n}}

为等差数列

C.

a_{n} = 2 n - 1

D.

\frac{1}{a_{1}} + \frac{1}{a_{2}} + \dots + \frac{1}{a_{2 n - 1}} = \frac{2 n - 1}{a_{n}}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 如图, 在四棱锥

P - A B C D

中, 底面

A B C D

为直角梯形,

P A ⊥

平面

A B C D, P A = A B = A D = 2 C D =

A B / / C D, A B ⊥ A D

, 已知点

M

在平面

P A D

上运动, 点

H

在平面

A B C D

上运动, 则下列说法正确的是

A.

若点

H

到

C D

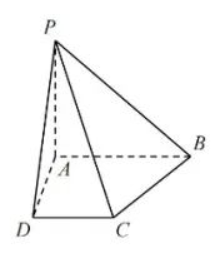
的距离等于其到平面

P A B

的距离, 则点

H

的轨迹为抛物线的一部分

B.

若

∠ B M A = ∠ C M D

, 则点

M

的轨迹为圆的一部分

C.

若

B M

与

B D

所成的角为

30^{\circ}

, 则点

M

的轨迹为椭圆的一部分

D.

若

C M

与平面

A B C D

所成的角为

30^{\circ}

, 则点

M

的轨迹为双曲线的一部分

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 3 题），请把答案直接填写在答题纸上

12. 集合

A = {\frac{15}{x + 2} \in Z | x \in N^{*}}

, 则

A

的真子集个数为

个。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 若曲线

y = \ln (x - 2) + 4

在

x = 3

处的切线也是曲线

y = x^{2} - x + a

的切线, 则

a =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 在

△ A B C

中, 内角

A, B, C

所对的边分别为

a, b, c

, 已知

c = 1, \frac{\sin B}{\sin A} = b^{2} - a^{2} + 1

, 且

a \neq b

, 则

\sin B - \sin A

的最大值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

15. 近几年, 我国促进新能源汽车产业发展的政策频出, 积极推动新能源汽车市场的迅速发展. 某新能源汽车公司为了解其对

A

型充电桩进行投资后所获得的利润

y

(单位: 百万元) 关于投资金额

x

(单位: 百万元) 之间的关系, 统计后得到 10 组样本数据, 根据统计数据计算得到

\sum_{i = 1}^{10} y_{i} = 40, \sum_{i = 1}^{10} x_{i}

= 70

, 利润的方差

S_{y}^{2} = 3.6

, 投资金额的方差

S_{x}^{2} = 12

, 以及样本相关系数

r = 0.96

.
(1) 根据样本相关系数

r

判断利润

y

与投资

x

的相关性强弱, 并求出

y

关于

x

的经验回归方程（精确到 0.01 ）;
(2) 为了解使用

A

型充电桩的车主性别与使用满意度 (分为满意与不满意) 的情况, 该公司又随机调查了该地区 150 名使用

A

型充电桩的车主, 其中男性车主有 60 名对

A

型充电桩的使用表示满意, 有 30 名对

A

型充电桩的使用表示不满意；女性车主中有

60 %

对

A

型充电桩的使用表示满意。将频率视为概率, 用样本估计总体. 已知该地区一位车主对

A

型充电桩的使用表示满意, 求这位车主是男性的概率.

附: (i) 样本相关系数

r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} \sqrt{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}

, 当

| r | \in [0.75, 1]

时, 相关性较强, 当

| r | \in

[0.3, 0.75)

时, 相关性一般;
(ii) 经验回归方程

\hat{y} = \hat{a} + \hat{b} x

中斜率和截距的最小二乘估计公式分别为

\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}, \hat{a} = \bar{y} - \hat{b} \bar{x}

;
(iii)

\sqrt{30} \approx 5.477

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 已知

{a_{n}}

是正项递增的等比数列, 且

a_{2} a_{6} = 64, a_{3} + a_{5} = 20

. 数列

{b_{n}}

是等差数列, 且

(n + 1) b_{n} =

2 n^{2} + n + C

.
(1) 分别求数列

{a_{n}}

和数列

{b_{n}}

的通项公式;
(2) 设

c_{n} = (- 1)^{n} a_{n} + \frac{1}{b_{n} b_{n + 1}}

, 求数列

{c_{n}}

前

n

项和

S_{n}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

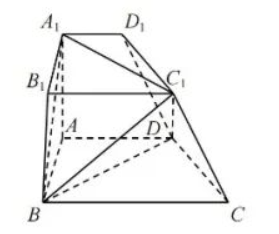
17. 如图, 在四棱台

A B C D - A_{1} B_{1} C_{1} D_{1}

中, 底面

A B C D

为等腰梯形,

A D / / B C

, 平面

A D D_{1} A_{1} ⊥

平面

A B C D

, 平面

A B B_{1} A_{1} ⊥

平面

A B C D

.
(1) 证明:

A A_{1} ⊥

平面

A B C

;
(2) 若

A B = A D = A A_{1} = 4, A_{1} B_{1} = 2, ∠ B A D = 120^{\circ}

, 求平面

A_{1} B C_{1}

与平面

D B C_{1}

夹角的余弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 已知双曲线

C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)

的左、右焦点分别为

F_{1}, F_{2}

, 且焦距为 4 , 左顶点为

E

, 过右焦点

F_{2}

的动直线

l

交

C

于

A, B

两点, 当

l

垂直于

x

轴时,

| A B | = 6

.
(1) 求

C

的方程;
(2) 若动直线

l

与

C

的左支交于点

A

, 右支交于点

B

, 求

\frac{S_{△ A E F}}{S_{△ B E F_{2}}}

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 设

y = f (x)

是定义域为

D

且图象连续不断的函数, 若存在区间

[a, b] \subseteq D

和

x_{0} \in (a, b)

, 使得

y = f (x)

在

[a, x_{0})

上单调递增, 在

(x_{0}, b]

上单调递减, 则称

y = f (x)

为 "山峰函数",

x_{0}

为 "峰点",

[a, b]

称为

y

= f (x)

的一个"峰值区间".
(1) 判断

g (x) = x^{2} + \cos x

是否是 "山峰函数"? 若是，请指出它的一个"峰值区间"；若不是，请说明理由；
(2) 已知

m > 1, h (x) = (m + 2) x - x^{2} - m^{x}

是"山峰函数", 且 [0,1] 是它的一个"峰值区间", 求

m

的取值范围；
(3) 设

n \in R

, 函数

I (x) = [x^{3} - 2 n x^{2} + (4 n - 4) x] \ln x - \frac{1}{3} x^{3} + n x^{2} - (4 n - 4) x

. 设函数

y = I (x)

是 "山峰函数",

[s, t]

是它的一个 "峰值区间", 并记

t - s

的最大值为

d (n)

. 若

I (\frac{2}{3}) < 0

, 且

I (\frac{2}{3}) ⩽ I (1), I (\frac{3}{2})

⩽ I (1)

, 求

d (n)

的最小值. (参考数据:

\ln \frac{3}{2} \approx 0.4)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。