单选题 (共 8 题 ),每题只有一个选项正确
某校高一年级 18 个班参加艺术节合唱比赛, 通过简单随机抽样, 获得了 10 个班的比赛得分如下: $91,89,90,92,94,87,93,96,91,85$, 则这组数据的 $80 \%$ 分位数为
$\text{A.}$ 93
$\text{B.}$ 93.5
$\text{C.}$ 94
$\text{D.}$ 94.5
若函数 $f(x)=\ln \left(x^2-a x\right)$ 在区间 $(2,5)$ 上单调递增, 则实数 $a$ 的取值范围是
$\text{A.}$ $(-\infty, 5]$
$\text{B.}$ $(-\infty, 2)$
$\text{C.}$ $(-\infty, 2]$
$\text{D.}$ $[5,+\infty)$
已知等差数列 $\left\{a_n\right\}$ 满足 $a_2+a_5+a_8=4$, 前 $n$ 项和为 $S_n$, 则 $S_9=$
$\text{A.}$ 8
$\text{B.}$ 12
$\text{C.}$ 16
$\text{D.}$ 24
甲、乙、丙等 5 名同学参加政史地三科知识竞赛, 每人随机选择一科参加竞赛, 则甲和乙不参加同一科, 甲和丙参加同一科竞赛, 且这三科竞赛都有人参加的概率为
$\text{A.}$ $\frac{4}{81}$
$\text{B.}$ $\frac{2}{27}$
$\text{C.}$ $\frac{10}{81}$
$\text{D.}$ $\frac{4}{27}$
已知椭圆 $\frac{x^2}{4}+y^2=1$, 点 $P$ 是椭圆上的任一点, 则点 $P$ 到直线 $x+2 y-\sqrt{2}=0$ 的最大距离是
$\text{A.}$ $3 \sqrt{10}$
$\text{B.}$ $\frac{6 \sqrt{10}}{5}$
$\text{C.}$ $\sqrt{10}$
$\text{D.}$ $\frac{3 \sqrt{10}}{5}$
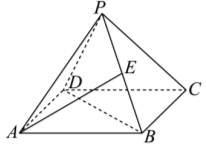
如图所示的四棱椎 $P-A B C D$ 中, 底面 $A B C D$ 为正方形, 且各棱长均相等, $E$ 是 $P B$ 的中点, 则异面直线 $A E$ 与 $B D$ 所成角的余弦值为
$\text{A.}$ $1$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\frac{\sqrt{6}}{6}$
已知函数 $f(x)=\frac{\cos x}{x}$, 若 ${A}, B$ 是锐角 $\triangle A B C$ 的两个内角, 则下列结论一定正确的是
$\text{A.}$ $f(\sin A)>f(\sin B)$
$\text{B.}$ $f(\cos A)>f(\cos B)$
$\text{C.}$ $f(\sin A)>f(\cos B)$
$\text{D.}$ $f(\cos A)>f(\sin B)$
实数 $a, b, c, d$ 满足 $(2 a-\sqrt{3} b+6)^2+\left(\sqrt{12-3 c^2}-2 d\right)^2=0$, 则 $(a-c)^2+(b-d)^2$ 的最小值为
$\text{A.}$ $\frac{1}{7}$
$\text{B.}$ $\frac{\sqrt{7}}{7}$
$\text{C.}$ $\frac{2 \sqrt{7}}{7}$
$\text{D.}$ $\frac{4}{7}$
多选题 (共 3 题 ),每题有多个选项正确
近年来, 中国电影行业发展迅猛, 消费者追求电影剧情的高质量, 重视电影内容正面传达的积极情绪, 并且愿意为其买单. 某机构调查到观众在观看电影时除了关注电影的剧情、情节外, 还会关注电影的幕后团队、精神内涵价值观、参演人员等方面. 如图所示为该机构调查的 2023 年中国网民观看电影时关注方面占比的统计表, 则下列结论正确的是
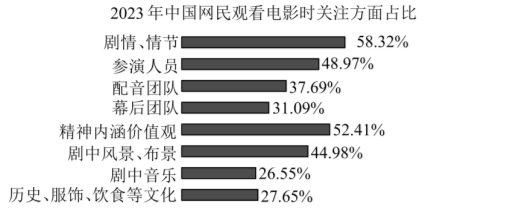
$\text{A.}$ 2023 年中国网民观看电影时超过 $40 \%$ 的网民会关注参演人员
$\text{B.}$ 这 8 个方面占比的极差是 $31.77 \%$
$\text{C.}$ 这 8 个方面占比的中位数为 $37.69 \%$
$\text{D.}$ 2023 年中国网民观看电影时至少有 $10.73 \%$ 的网民既关注剧情、情节, 又关注精神内涵价值观
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathrm{R}$, 若 $f(x)$ 是奇函数, $f(2)=-f(1) \neq 0$, 且对任意 $x, y \in \mathrm{R}, f(x+y)=f(x) f^{\prime}(y)+f^{\prime}(x) f(y)$, 则
$\text{A.}$ $f^{\prime}(1)=\frac{1}{2}$
$\text{B.}$ $f(9)=0$
$\text{C.}$ $\sum_{k=1}^{20} f(k)=1$
$\text{D.}$ $\sum_{k=1}^{20} f^{\prime}(k)=-1$
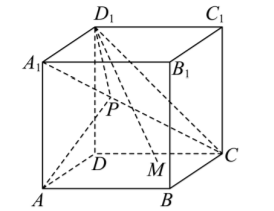
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $P$ 为线段 $A_1 C$ 上的动点, 则下列结论正确的是
$\text{A.}$ 当 $\overrightarrow{A_1 P}=\frac{1}{3} \overrightarrow{A_1 C}$ 时, $\overrightarrow{D_1 P} \cdot \overrightarrow{A P}$ 的值最小
$\text{B.}$ 当 $\overrightarrow{A_1 P}=\frac{2}{3} \overrightarrow{A_1 C}$ 时, $\overrightarrow{D_1 P} \perp \overrightarrow{A P}$
$\text{C.}$ 若平面 $A B C D$ 上的动点 $M$ 满足 $\angle M D_1 C=\frac{\pi}{6}$, 则点 $M$ 的轨迹是椭圆
$\text{D.}$ 直线 $D D_1$ 与平面 $A_1 D_1 P$ 所成角的正弦值是 $\frac{1}{2}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
已知集合 $A=\left\{a-2, a^2+4 a, 10\right\}$, 且 $-3 \in A$, 则 $a=$
设等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_n=2^{n+1}+\lambda$, 则实数 $\lambda=$
为求方程 $x^5-1=0$ 的虚根, 可把原式变形为 $(x-1)\left(x^2+a x+1\right)\left(x^2+b x+1\right)=0$, 由此可得原方程的一个虚根的实部为
已知函数 $f(x)=x^3+a x^2+b x+c$ 在 $x=-1$ 和 $x=3$ 处取得极值.
(1)求 $a, b$ 的值及 $f(x)$ 的单调区间;
(2) 若对任意 $x \in[1,5]$, 不等式 $f(x) < c^2$ 恒成立, 求 $c$ 的取值范围.
某面包店的面包师声称自己店里所出售的每个面包的质量均服从期望为 $1000 \mathrm{~g}$, 标准差为 $50 \mathrm{~g}$ 的正态分布.
(1)已知如下结论: 若 $X \sim N\left(\mu, \sigma^2\right)$, 从 $X$ 的取值中随机抽取 $K\left(K \in \mathbf{N}^*, K \geq 2\right)$ 个数据, 记这 $K$ 个数据的平均值为 $Y$, 则随机变量 $Y \sim N\left(\mu, \frac{\sigma^2}{K}\right)$, 请利用该结论解决问题; 假设面包师的说法是真实的, 那么从面包店里随机购买 25 个面包, 记这 25 个面包质量的平均值为 $Y$, 求 $P(Y < 980)$;
(2)假设有两箱面包 (面包除颜色外, 其它都一样), 已知第一箱中共装有 6 个面包, 其中黄色面包有 2 个; 第二箱中共装有 8 个面包, 其中黄色面包有 3 个, 现随机挑选一箱, 然后从该箱中随机取出 2 个面包, 求取出黄色面包个数的分布列及数学期望.
附:随机变量 $\eta$ 服从正态分布 $N\left(\mu, \sigma^2\right)$, 则 $P(\mu-\sigma \leq \eta \leq \mu+\sigma)=0.6827$,
$$
P(\mu-2 \sigma \leq \eta \leq \mu+2 \sigma)=0.9545, \quad P(\mu-3 \sigma \leq \eta \leq \mu+3 \sigma)=0.9973 \text {. }
$$
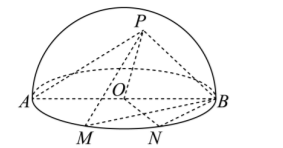
如图, $A B$ 是半球 $O$ 的直径, $A B=4, M, N$ 依次是底面 $A B$ 上的两个三等分点, $P$ 是半球面上一点, 且 $\angle P O N=60^{\circ}$.
(1)证明: $P B \perp P M$;
(2)若点 $P$ 在底面圆上的射影为 $O N$ 中点, 求直线 $P M$ 与平面 $P A B$ 所成的角的正弦值.
(1)证明: $P B \perp P M$;
(2)若点 $P$ 在底面圆上的射影为 $O N$ 中点, 求直线 $P M$ 与平面 $P A B$ 所成的角的正弦值.
已知双曲线 $C$ 的中心为坐标原点, 对称轴为坐标轴, 点 $P(2,2)$ 在 $C$ 上, 点 $P$ 与 $C$ 的上、下焦点连线所在直线的斜率之积为 $-\frac{1}{2}$.
(1)求双曲线 $C$ 的标准方程;
(2)经过点 $A(0,1)$ 的直线 $l_1$ 与双曲线 $C$ 交于 $E, F$ 两点(异于点 $P$ ), 过点 $F$ 作平行于 $x$ 轴的直线 $l_2$, 直线 $P E$ 与 $l_2$ 交于点 $D$, 且 $\overrightarrow{D F}=2 \overrightarrow{B F}$ 求直线 $A B$ 的斜率.
(本题满分17分)记 $U=\{1,2, \ldots, 100\}$. 对数列 $\left\{\mathrm{a}_{\mathrm{n}}\right\}\left(\mathrm{n} \in \mathrm{N}^*\right)$ 和 $\mathrm{U}$ 的子集 $T$, 若 $\mathrm{T}=\varnothing$, 定义 $\mathrm{S}_{\mathrm{T}}=0$;
若 $\mathrm{T}=\left\{\mathrm{t}_1, \mathrm{t}_2, \ldots, \mathrm{t}_{\mathrm{k}}\right\}$, 定义 $\mathrm{S}_{\mathrm{T}}=\mathrm{a}_{\mathrm{t} 1}+\mathrm{a}_{\mathrm{t} 2}+\ldots+\mathrm{a}_{\mathrm{tk}}$. 例如: $\mathrm{T}=\{1,3,66\}$ 时, $\mathrm{S}_{\mathrm{T}}=\mathrm{a}_1+\mathrm{a}_3$ $+a_{66}$. 现设 $\left\{a_n\right\}\left(n \in N^*\right)$ 是公比为 3 的等比数列, 且当 $T=\{2,4\}$ 时, $S_T=30$.
(1) 求数列 $\left\{\mathrm{a}_{\mathrm{n}}\right\}$ 的通项公式;
(2) 对任意正整数 $\mathrm{k}(1 \leq \mathrm{k} \leq 100)$, 若 $\mathrm{T}\{1,2, \ldots, \mathrm{k}\}$, 求证: $\mathrm{S}_{\mathrm{T}} < \mathrm{a}_{\mathrm{k}}+1$;
(3) 设 $\mathrm{C} \subseteq \mathrm{U}, \mathrm{D} \subseteq \mathrm{U}, \mathrm{SC} \geq \mathrm{SD}$, 求证: $\mathrm{S}_{\mathrm{C}}+\mathrm{S}_{\mathrm{C} \cap \mathrm{D}} \geq 2 \mathrm{~S}_{\mathrm{D}}$.