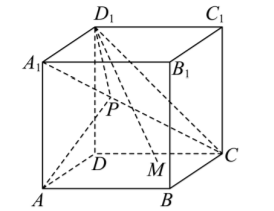
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $P$ 为线段 $A_1 C$ 上的动点, 则下列结论正确的是
A
当 $\overrightarrow{A_1 P}=\frac{1}{3} \overrightarrow{A_1 C}$ 时, $\overrightarrow{D_1 P} \cdot \overrightarrow{A P}$ 的值最小
B
当 $\overrightarrow{A_1 P}=\frac{2}{3} \overrightarrow{A_1 C}$ 时, $\overrightarrow{D_1 P} \perp \overrightarrow{A P}$
C
若平面 $A B C D$ 上的动点 $M$ 满足 $\angle M D_1 C=\frac{\pi}{6}$, 则点 $M$ 的轨迹是椭圆
D
直线 $D D_1$ 与平面 $A_1 D_1 P$ 所成角的正弦值是 $\frac{1}{2}$
E
F