单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\left\{x \mid x^2-3 x+2>0\right\}, B=\left\{x \mid \frac{1}{x+1} \geqslant 1\right\}$, 则 $A \cap\left(C_R B\right)=$
$\text{A.}$ $(0,1) \cup(2,+\infty)$
$\text{B.}$ $(-\infty,-1] \cup(2,+\infty)$
$\text{C.}$ $(-\infty,-1) \cup(0,1) \cup(2,+\infty)$
$\text{D.}$ $(-\infty,-1] \cup(0,1) \cup(2,+\infty)$
已知 $\frac{z+1}{z-1}=\sqrt{3} \mathrm{i}$, 则 $\bar{z}=$
$\text{A.}$ $\frac{1}{2}+\frac{\sqrt{3}}{2} \mathrm{i}$
$\text{B.}$ $-\frac{1}{2}+\frac{\sqrt{3}}{2} \mathrm{i}$
$\text{C.}$ $-\frac{1}{2}-\frac{\sqrt{3}}{2} \mathrm{i}$
$\text{D.}$ $\frac{1}{2}-\frac{\sqrt{3}}{2} \mathrm{i}$
已知圆锥的母线长为 1 , 其侧面展开图是一个圆心角为 $120^{\circ}$ 的扇形, 则该圆锥的轴截面面积为
$\text{A.}$ $\frac{2 \sqrt{5}}{9}$
$\text{B.}$ $\frac{2 \sqrt{2}}{9}$
$\text{C.}$ $\frac{\sqrt{5}}{9}$
$\text{D.}$ $\frac{\sqrt{2}}{9}$
下列区间中, 函数 $f(x)=3 \sin \left(\frac{\pi}{3}-2 x\right)$ 单调递增的区间是
$\text{A.}$ $\left(0, \frac{\pi}{4}\right)$
$\text{B.}$ $\left(\frac{\pi}{4}, \frac{\pi}{2}\right)$
$\text{C.}$ $\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right)$
$\text{D.}$ $\left(\frac{3 \pi}{4}, \pi\right)$
若 $\tan \theta=-2$, 且 $\theta \in\left(\frac{3 \pi}{2}, 2 \pi\right)$, 则 $\sin \theta+\cos \theta=$
$\text{A.}$ $\frac{3 \sqrt{5}}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{5}$
$\text{C.}$ $-\frac{\sqrt{5}}{5}$
$\text{D.}$ $-\frac{3 \sqrt{5}}{5}$
已知直线 $l$ 过抛物线 $C: y^2=4 x$ 的焦点 $F$, 与抛物线 $C$ 交于 $A B$ 两点, 且 $|A B|,|A F|,|B F|$ 成等差 数列, 则直线$l$ 的斜率 $k=$
$\text{A.}$ $\pm 1$
$\text{B.}$ $\pm \sqrt{2}$
$\text{C.}$ $\pm 2$
$\text{D.}$ $\pm 2 \sqrt{2}$
若过点 $(a, b)(a>0)$ 可以作物线 $y=x^3-3 x$ 的三条切线, 则
$\text{A.}$ $b < -3 a$
$\text{B.}$ $-3 a < b < a^3$
$\text{C.}$ $b>a^3-3 a$
$\text{D.}$ $b=-3 a$ 或 $b=a^3-3 a$
甲、乙, 丙、丁等六名退休老党员相约去观看党史舞台剧 《星火》. 《星火》的票价为 50 元 / 人, 每人 限购一张票. 甲、乙、丙三人各带了一张 50 元钞, 其余三人各带了一张 100 元钞. 他们六人排成一列到 售票处买票, 而售票处一开始没有准备 50 元零钱, 那么他们六人共有多少种不同排队顺序能使购票时售 票处不出现找不出钱的状态.
$\text{A.}$ 720
$\text{B.}$ 360
$\text{C.}$ 180
$\text{D.}$ 90
多选题 (共 4 题 ),每题有多个选项正确
某高中有学生 500 人, 其中男生 300 人, 女生 200 人, 希望获得全体学生的身高信息, 按照分层抽样 的原则抽取了容量为 50 的样本. 经计算得到男生身高样本均值为 $170 \mathrm{~cm}$, 方差为 $17 \mathrm{~cm}^2$; 女生身高样本均 值为 $160 \mathrm{~cm}$, 方差为 $30 \mathrm{~cm}^2$. 下列说法中正确的是
$\text{A.}$ 男生样本量为 30
$\text{B.}$ 每个女生人样的概率均为 $\frac{2}{5}$
$\text{C.}$ 所有样本的均值为 $166 \mathrm{~cm}$
$\text{D.}$ 所有样本的方差为 $22.2 \mathrm{~cm}^2$
已知 $\overrightarrow{O A} \cdot \overrightarrow{O B}=|\overrightarrow{O A}|=\frac{1}{2}|\overrightarrow{O B}|=1$, 点 $P$ 满足 $\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}(x, y \in \mathbf{R})$, 则下列说法中正确的是
$\text{A.}$ 当 $x+y=1$ 时, $\overrightarrow{O P} \mid$ 的最小值为 1
$\text{B.}$ 当 $x^2+y^2=1$ 时, $|\overrightarrow{O P}|=1$
$\text{C.}$ 当 $x=\frac{1}{2}$ 时, $\triangle A B P$ 的面积为定值
$\text{D.}$ 当 $y=\frac{1}{2}$ 时, $|\overrightarrow{A P}|=|\overrightarrow{B P}|$
已知点 $P$ 在圆 $C:(x-4)^2+(y-5)^2=5$ 上, 点 $A(4,0), B(0,2)$, 则下列说法中正确的是
$\text{A.}$ 点 $P$ 到直线 $A B$ 的距离小于 6
$\text{B.}$ 点 $P$ 到直线 $A B$ 的距离大于 2
$\text{C.}$ $\cos \angle A P B$ 的最大值为 $\frac{4}{5}$
$\text{D.}$ $\angle A P B$ 的最大值为 $\frac{\pi}{2}$
已知函数 $f(x)=\ln x+1-a x$ 有两个零点 $x_1, x_2\left(x_1 < x_2\right)$, 则
$\text{A.}$ $a$ 的取值范围为 $(-\infty, 1)$
$\text{B.}$ $x_1+x_2-x_1 x_2>1$
$\text{C.}$ $x_1+x_2>2$
$\text{D.}$ $\frac{1}{x_1}+\frac{1}{x_2}>2$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)=\frac{a^x}{3^x+1}(a>0, a \neq 1)$ 是偶函数, 则 $f(x)$ 的最大值为
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左顶点为 $A$, 上顶点为 $B$, 右焦点为 $F$, 且 $\triangle A B F$ 是等腰三角 形, 则椭圆 $C$ 的离心率为
$\left(3 x^2+2 x+1\right)^{10}$ 的展开式中, $x^2$ 项的系数为
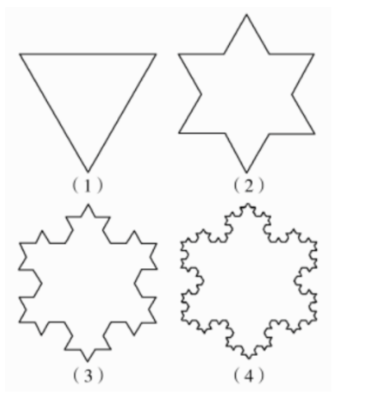
将正三角形 (1) 的每条边三等分, 并以中间的那一条 线段为底边向外作正三角形, 然后去掉底边, 得到图 (2); 将图 (2) 的每条边三等分, 并以中间的那一条线段为底边 向外作正三角形, 然后去掉底边, 得到图(3); 如此类推, 将图 $(n)$ 的每条边三等分, 并以中间的那一条线段为底边 向外作三角形, 然后去掉底边, 得到图 $(n+1)$. 上述作 图过程不断的进行下去, 得到的曲线就是美丽的雪花曲 线. 若图 (1) 中正三角形的边长为 1 , 则图 $(n)$ 的周长为 ________ , 图 $(n)$ 的面积为 ________
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 满足 $a_1=1, a_n+a_{n-1}=2 n\left(n \geqslant 2, n \in \mathrm{N}^*\right)$.
(1) 记 $b_n=a_{2 n}$, 求数列 $\left\{b_n\right\}$ 的通项公式;
(2) 求数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n$.
有专家指出, 与新冠病毒感染者密切接触过的人, 被感染的概率是 $9 \%$. 王某被确诊为新冠病毒感染 者后, 当地准备对王某的密切接触者共 78 人逐一进行核酸检测.
(1) 设 $X$ 为这 78 名密切接触者中被感染的人数, 求 $X$ 的数学期望;
(2) 核酸检测并不是 $100 \%$ 准确, 有可能出现假阴性(新冠病毒感染者的检测结果为阴性, 即漏诊) 或假阳性 (非新冠病毒感染者的检测结果为阳性, 即误诊). 假设当地核酸检测的灵敏度为 $98 \%$ (即假阴 性率为 $2 \%$ ), 特异度为 $99 \%$ (即假阳性率为 $1 \%$ ). 已知王某的一个密切接触者赵某的核酸检测结果为阳 性, 求他被感染的概率 (结果保留 3 位有效数字).
已知 $\triangle A B C$ 中, $\angle A B C=\frac{\pi}{3}, \angle A B C$ 的平分线交 $A C$ 于点 $D, B D=2 \sqrt{3}$.
(1) 若 $A D=2 D C$, 求 $A C$ 的长度;
(2) 求 $\triangle A B C$ 面积的最小值.
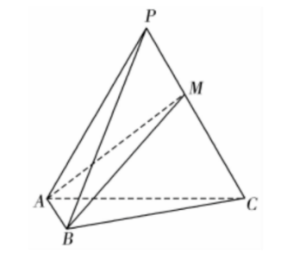
如图, 在三棱锥 $P-A B C$ 中, 侧面 $P A C$ 是等边三角形, $A B \perp B C, P A=P B$.
(1) 证明: 平面 $P A C \perp$ 平面 $A B C$;
(2) 若 $A C=2 A B$, 点 $M$ 在棱 $P C$ 上, 且二面角 $M-A B-C$ 的大小为 $45^{\circ}$, 求 $\frac{P M}{P C}$.
在平面直角坐标系 $x O y$ 中, 已知动点 $P$ 到点 $F(2,0)$ 的距离与它到直线 $x=\frac{3}{2}$ 的距离之比为 $\frac{2 \sqrt{3}}{3}$. 记点 $P$ 的轨迹为曲线 $C$.
(1) 求曲线 $C$ 的方程;
(2) 过点 $F$ 作两条互相垂直的直线 $l_1, l_2, l_1$ 交曲线 $C$ 于 $A, B$ 两点, $l_2$ 交曲线 $C$ 于 $S, T$ 两点, 线段 $A B$ 的 中点为 $M$, 线段 $S T$ 的中点为 $N$. 证明:直线 $M N$ 过定点, 并求出该定点坐标.
已知函数 $f(x)=\log _a x$, 其中 $0 < a < 1$.
(1) 若不等式 $f(x) \geqslant 1-x$ 恒成立, 求实数 $a$ 的值;
(2) 讨论方程 $f(x)=a^x$ 的解的个数.