单选题 (共 5 题 ),每题只有一个选项正确
在长方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$A B=B C=1, A A_1=\sqrt{3}$ ,则异面直线 $A D_1$ 与 $D B_1$ 所成角的余弦值为
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{6}$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
已知 $A(1,0,0), B(0,1,0), C(0,0,1)$ ,则下列向量是平面 $A B C$ 法向量的是( )
$\text{A.}$ $(-1,1,1)$
$\text{B.}$ $(1,-1,1)$
$\text{C.}$ $\left(-\frac{\sqrt{3}}{3},-\frac{\sqrt{3}}{3},-\frac{\sqrt{3}}{3}\right)$
$\text{D.}$ $\left(\frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3},-\frac{\sqrt{3}}{3}\right)$
若直线 $l$ 的方向向量为 $a =(1,0,2)$ ,平面 $\alpha$ 的法向量为 $n =(-2,1,1)$ ,则 ()
$\text{A.}$ $l / / \alpha$
$\text{B.}$ $l \perp \alpha$
$\text{C.}$ $l \subset \alpha$ 或 $l / / \alpha$
$\text{D.}$ $l$ 与 $\alpha$ 斜交
已知两平面的法向量分别为 $m =(0,1,0), n =(0,1,1)$ ,则两平面所成的二面角为( )
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $135^{\circ}$
$\text{C.}$ $45^{\circ}$ 或 $135^{\circ}$
$\text{D.}$ $90^{\circ}$
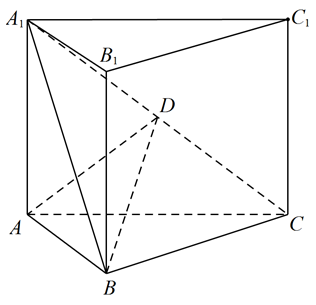
在直三棱柱 $A B C-A_1 B_1 C_1$ 中,$\angle B C A=90^{\circ}, M, N$ 分别是 $A_1 B_1, A_1 C_1$ 的中点,$B C=C A$ $=C C_1$ ,则 $B M$ 与 $A N$ 所成角的余弦值为()
$\text{A.}$ $\frac{1}{10}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{\sqrt{30}}{10}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
多选题 (共 1 题 ),每题有多个选项正确
在正三棱柱 $A B C-A_1 B_1 C_1$ 中,$A B=A A_1=1$ ,点 $P$ 满足 $\overrightarrow{B P}=\lambda \overrightarrow{B C}+\mu \overrightarrow{B B_1}$ ,其中 $\lambda \in[0,1], \mu \in[0,1]$ ,则( )
$\text{A.}$ 当 $\lambda=1$ 时,$\triangle A B_1 P$ 的周长为定值
$\text{B.}$ 当 $\mu=1$ 时,三棱锥 $P-A_1 B C$ 的体积为定值
$\text{C.}$ 当 $\lambda=\frac{1}{2}$ 时,有且仅有一个点 $P$ ,使得 $A_1 P \perp B P$
$\text{D.}$ 当 $\mu=\frac{1}{2}$ 时,有且仅有一个点 $P$ ,使得 $A_1 B \perp$ 平面 $A B_1 P$
解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
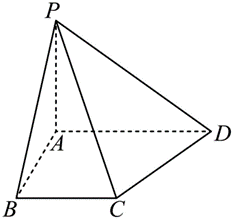
在四棱锥 $P-A B C D$ 中,$P D \perp$ 底面 $A B C D, C D \| A B, A D=D C=C B=1, A B=2, D P=\sqrt{3}$ .
(1)证明:$B D \perp P A$ ;
(2)求 $P D$ 与平面 $P A B$ 所成的角的正弦值.
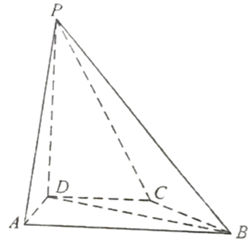
如图,四面体 $A B C D$ 中,$A D \perp C D, A D=C D, \angle A D B=\angle B D C, E$ 为 $A C$ 的中点.
(1)证明:平面 $B E D \perp$ 平面 $A C D$ ;
(2)设 $A B=B D=2, \angle A C B=60^{\circ}$ ,点 $F$ 在 $B D$ 上,当 $\triangle A F C$ 的面积最小时,求 $C F$ 与平面 $A B D$ 所成的角的正弦值。
如图,直三棱柱 $A B C-A_1 B_1 C_1$ 的体积为 $4, \triangle A_1 B C$ 的面积为 $2 \sqrt{2}$ .
(1)求 $A$ 到平面 $A_1 B C$ 的距离;
(2)设 $D$ 为 $A_1 C$ 的中点,$A A_1=A B$ ,平面 $A_1 B C \perp$ 平面 $A B B_1 A_1$ ,求二面角 $A-B D-C$ 的正弦值.
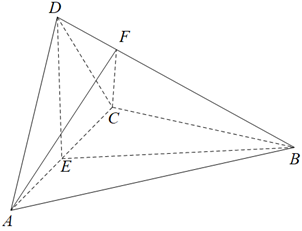
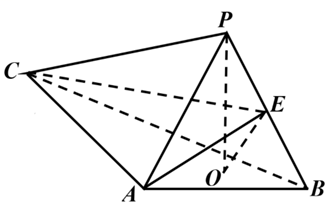
如图,$P O$ 是三棱锥 $P-A B C$ 的高,$P A=P B, A B \perp A C, E$ 是 $P B$ 的中点.
(1)证明:$O E / /$ 平面 $P A C$ ;
(2)若 $\angle A B O=\angle C B O=30^{\circ}, P O=3, P A=5$ ,求二面角 $C-A E-B$ 的正弦值.
如图,在四棱锥 $P-A B C D$ 中,底面 $A B C D$ 是矩形,$P A \perp$ 底面 $A B C D, E$ 是 $P C$ 的中点.已知 $A B=2, A D=2 \sqrt{2}, P A=2$ ,求异面直线 $B C$ 与 $A E$ 所成的角的大小.
如图,在多面体 $A B C D E F$ 中,四边形 $A B C D$ 是菱形,$E F / / A C, E F=1, \angle A B C=60^{\circ}, C E \perp$ 平面 $A B C D, C E=\sqrt{3}, C D_{=2}, G$ 是 $D E$ 的中点.
(1)求证:平面 $A C G / /$ 平面 $B E F$ ;
(2)求直线 $A D$ 与平面 $A B F$ 所成的角的正弦值.

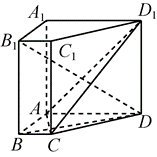
如图,在直棱柱 $A B C D-A_1 B_1 C_1 D_1$ 中,$A D / / B C, \angle B A D=90^{\circ}, A C \perp B D, B C=1, A D=A A_1$ $=3$ 。
(1)求证:$A C \perp B_1 D$ ;
(2)求直线 $B_1 C_1$ 与平面 $A C D_1$ 所成角的正弦值.
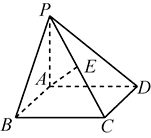
如图,在四棱锥 $P-A B C D$ 中,$A P \perp$ 平面 $P C D, A D / / B C, A B \perp B C, A P=A B=B C=\frac{1}{2} A D$ , $E$ 为 $A D$ 的中点,$A C$ 与 $B E$ 相交于点 $O$ .
(1)证明:$P O \perp$ 平面 $A B C D$ .
(2)求直线 $B C$ 与平面 $P B D$ 所成角的正弦值.
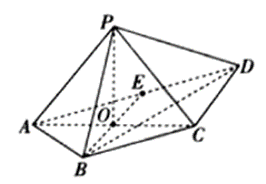
如图,在四棱锥 $P-A B C D$ 中,底面四边形 $A B C D$为菱形,点 $E$ 为棱 $P D$ 的中点,$O$ 为边 $A B$ 的中点.(1)求证:$A E \|$ 平面 $P O C$ ;
(2)若侧面 $P A B \perp$ 底面 $A B C D$ ,且 $\angle A B C=\angle P A B=\frac{\pi}{3}, A B=2 P A=4$ ,求平面 $P A D$ 与平面 $P O C$ 的夹角的余弦值.
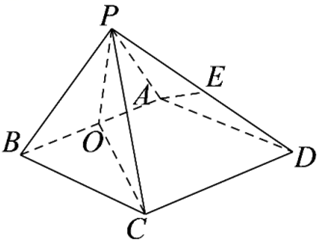
如图,在棱长均为 2 的三棱柱 $A B C-A_1 B_1 C_1$ 中,平面 $A_1 C B \perp$ 平面 $A_1 A B B_1, A B_1=A_1 B, O$ 为 $A B_1$ 与 $A_1 B$ 的交点.(1)求证:$A B_1 \perp C O$ ;
(2)求平面 $A C C_1 A_1$ 与平面 $A B C$ 所成锐二面角的余弦值.
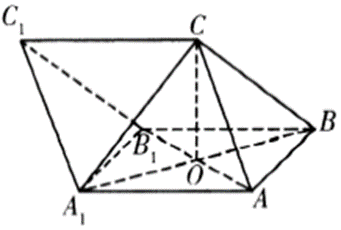
已知四棱锥 $P-A B C D$ ,底面 $A B C D$ 是梯形,$A D / / B C, A B=B C=2, \angle A B C=60^{\circ}, C D \perp A C$ ,平面 $P A B \perp$ 平面 $A B C D$ ,且 $P A=A D, P B=2 \sqrt{5}, E$ 为 $P D$ 中点,$A F \perp P C$ ,垂足为 $F$ .
(1)求证:$P A \perp$ 平面 $A B C D$ ;
(2)求异面直线 $A B$ 与 $C E$ 所成的角;
(3)求证:$P D \perp E F$ .
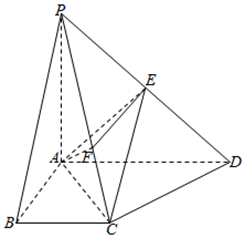
如图,已知四棱锥 $P-A B C D$ 的底面 $A B C D$ 是直角梯形,$A D / / B C, A D=4, \angle A B C=90^{\circ}, P A \perp$ 平面 $A B C D, P A=A B=B C=2$ ,
(1)求 $P B$ 与 $C D$ 所成的角
(2)平面 $P C D$ 与平面 $P B A$ 所成的锐二面角余弦值