一、单选题 (共 4 题 ),每题只有一个选项正确
1. 设 三个事件两两独立, 则 相互独立的充分必要条件是
与 独立.
与 独立.
与 独立.
与 独立.
2. 假设随机变量 与 相互独立且都服从参数为 的指数分布, 则下列变量中服从参数为 的指数分布的是
.
.
.
.
3. 设总体 服从正态分布 为来自总体 的简单随机样本,据此样本检测:假设 ,则
如果在检验水平 下拒绝 , 那么在检验水平 下必拒绝 。
如果在检验水平 下拒绝 , 那么在检验水平 下必接受 。
如果在检验水平 下接受 , 那么在检验水平 下必拒绝 .
如果在检验水平 下接受 , 那么在检验水平 下必接受 .
4. 设 是简单随机样本, 来自总体 , 其中 是未知参数, 则以下是统计量的是()。
二、填空题 (共 4 题 ),请把答案直接填写在答题纸上
5. 设 是来自正态总体 的样本, 样本均值为 , 则在显著性水平 下检验假设 的拒绝域为 .
6. 设随机变量 , 即 且相关系数 ,
则 ;
7. 已知二维随机变量
的分布律为
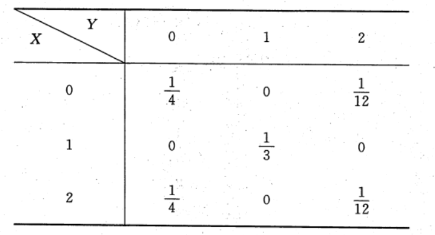
则
8. 已知二维随机变量 在矩形区域 上服从均匀分布, 则
三、解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
9. 某保险公司把被保险人分为 3 类: “谨傎的”、“一般的”、“冒失的”, 统计资料表明, 这 3种人在一年内发生事故的概率依次为 ; 如果 “谨慎的” 被保险人占 , “一般的占 , “冒失的” 占 , 问:
(1) 一个被保险人在一年内出事故的概率是多大?
(2) 若已知某被保险人出了事故, 求他是 “谨慎的” 类型的概率。
10. 已知 .
(1) 求随机变量 的分布函数;
(2) 设 是总体 的简单随机样本, 若 已知, 求参数 的矩估计量;
(3) 若 未知, 求参数 与 的最大似然估计量.
11. 设二维连续型随机变量 的概率密度为
其他
求随机变量 的概率密度.
12. 设连续型随机变量 的密度函数为:
其它
求:
1) ;
2) 的密度函数 ;
3) ;
13. 设二维离散型随机变量
的概率分布的部分数据如下:
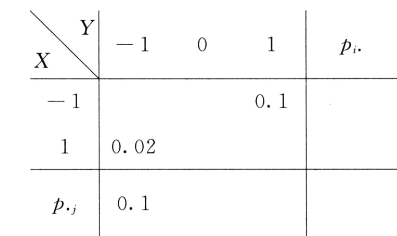
已知
, 且
与
不相关.
(I) 试将分布中的其余数据填人空白处;
(II) 试问
与
是否独立?
(III) 求
.
14. 在针织品漂白工艺过程中, 需要考察温度对针织品断裂强度的影响。假设在 80 摄氏度时, 针织品的断裂强度服从正态分布 , 现获得来自该总体的一个简单样本 , 其样本值为:
(1) 求 的置信水平为 0.9 的置信区间; (2) 如果 时, 认为该批次针织品的断裂强度是稳定的, 在显著性水平为 0.05 时, 通过该样本值判断针织品的断裂强度是否稳定.
上分位数表 。
15. 设 为来自总体 的简单随机样本, 的概率密度为
(I) 求参数 的矩估计量 ;
(II) 求参数 的最大似然估计量 ;
(III) 判断 是否为 的无偏估计量, 并说明理由.