设二维离散型随机变量 $(X, Y)$ 的概率分布的部分数据如下:
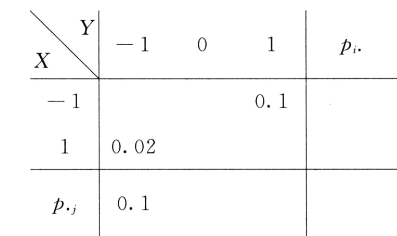
已知 $E(X)=0$, 且 $X$ 与 $Y$ 不相关.
(I) 试将分布中的其余数据填人空白处;
(II) 试问 $X$ 与 $Y$ 是否独立?
(III) 求 $\operatorname{Cov}\left(X, Y^2\right)$.

已知 $E(X)=0$, 且 $X$ 与 $Y$ 不相关.
(I) 试将分布中的其余数据填人空白处;
(II) 试问 $X$ 与 $Y$ 是否独立?
(III) 求 $\operatorname{Cov}\left(X, Y^2\right)$.