单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $M=\left\{y \mid y=2^x\right\}, N=\left\{y \mid y=\sqrt{1-x^2}\right\}$, 则 $M \cap N=$
$\text{A.}$ $\{x \mid 0 < x < 1\}$
$\text{B.}$ $\{x \mid 0 < x \leqslant 1\}$
$\text{C.}$ $\{x \mid x \leqslant 1\}$
$\text{D.}$ $\{x \mid x>0\}$
若 $z(1+2 \mathrm{i})=2-\mathrm{i}$ (i 为虚数单位), 则复数 $z=$
$\text{A.}$ $-i$
$\text{B.}$ $i$
$\text{C.}$ $1$
$\text{D.}$ $-1$
已知向量 $a=(-2, m), b=(1,-2)$, 若 $a \perp b$, 则 $m$ 的值为
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ 2
$\text{D.}$ -2
若 $a=0.7^{-0.5}, b=\log _{0.5} 0.7, c=\log _{0. 7} 5$, 则
$\text{A.}$ $b < a < c$
$\text{B.}$ $a < b < c$
$\text{C.}$ $c < a < b$
$\text{D.}$ $c < b < a$
某滑冰馆统计了 2021 年 11 月 1 日到 30 日某小区居民在该滑冰馆的锻炼天数, 得到如图所示的频率分布直方图(将频率视为概率), 则下列说法正确的是
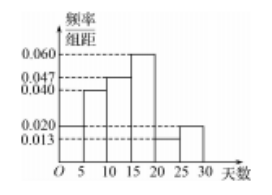
$\text{A.}$ 该小区居民在该滑冰馆的锻炼天数在区间 $(25,30]$ 内的最少
$\text{B.}$ 估计该小区居民在该滑冰馆的锻炼天数的中位数为 16
$\text{C.}$ 估计该小区居民在该滑冰馆的锻炼天数的平均值大于 14
$\text{D.}$ 估计该小区居民在该滑冰馆的锻炼天数超过15天的概率为0.456
已知等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $a_3+a_5=-10, S_6=-42$, 则 $S_{10}=$
$\text{A.}$ 6
$\text{B.}$ 10
$\text{C.}$ 12
$\text{D.}$ 20
“ $m=-1$ "是“直线 $l_1: m x+2 y+1=0$ 与直线 $l_2: \frac{1}{2} x+m y+\frac{1}{2}=0$ 平行" 的
$\text{A.}$ 充要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充分不必要条件
$\text{D.}$ 即不充分也不必要条件
若曲线 $y=\ln x+x^2$ 的一条切线的斜率为 3 , 则该切线的方程可能为
$\text{A.}$ $3 x-y-1=0$
$\text{B.}$ $3 x-y+1=0$
$\text{C.}$ $3 x-y-2=0$
$\text{D.}$ $3 x-y-1-\ln 2=0$
函数 $f(x)=\tan \left(2 x-\frac{\pi}{3}\right)$ 的图象的一个对称中心为
$\text{A.}$ $\left(\frac{\pi}{12}, 0\right)$
$\text{B.}$ $\left(\frac{7 \pi}{12}, 0\right)$
$\text{C.}$ $\left(-\frac{5 \pi}{12}, 0\right)$
$\text{D.}$ $\left(-\frac{\pi}{12}, 0\right)$
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $A B=2, P$ 为 $C C_1$ 的中点, 点 $Q$ 在四边形 $D C C_1 D_1$ 内 (包括边界)运动, 若 $A Q / /$ 平面 $A_1 B P$, 则 $A Q$ 的最小值为
$\text{A.}$ $1$
$\text{B.}$ $\frac{3 \sqrt{2}}{2}$
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $\sqrt{7}$
已知点 $M$ 在抛物线 $C: y^2=2 p x(p>0)$ 上, 若以点 $M$ 为圆心半径为 5 的圆与抛物线 $C$ 的准 线相切, 且与 $x$ 轴相交的弦长为 6 , 则 $p=$
$\text{A.}$ 2
$\text{B.}$ 8
$\text{C.}$ 2 或 8
$\text{D.}$ 6
已知函数 $y=f(x+1)$ 的图象关于直线 $x=-3$ 对称, 且对 $\forall x \in \mathbf{R}$ 都有 $f(x)+f(-x)=$ 2. 当 $x \in(0,2]$ 时, $f(x)=x+2$. 则 $f(2022)=$
$\text{A.}$ $-1$
$\text{B.}$ $1$
$\text{C.}$ $2$
$\text{D.}$ $-2$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$\left(x-\frac{1}{x}\right)^4$ 的展开式中的常数项为
已知 $0 < \alpha < \frac{\pi}{2}, \sin \alpha=\frac{3}{5}, \tan (\alpha-\beta)=-\frac{1}{3}$, 则 $\tan \beta=$
已知正四棱椎 $P-A B C D$ 的底面边长为 3 , 高为 2 ,若该四棱锥的五个顶点都在一个球面上, 则球心到四棱锥侧面的距离为
已知双曲线 $C: \frac{x^2}{6}-\frac{y^2}{3}=1$ 的右焦点为 $F_2$, 过点 $F_2$ 斜率为 $k$ 的直线 $l$ 与双曲线C 的右支交于$A, B$ 两点, 点 $P(-2 \sqrt{3}, 0)$, 若 $\triangle A B P$ 的外心 $Q$ 的横坐标为 0 , 则直线 $l$ 的方程为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 满足 $a_1=1, a_{n+1}=3 a_n (n \in \mathbf{N}^*)$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2)证明: $\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n} < \frac{3}{2}$.
已知 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别是 $a, b, c$, 满足 $\frac{a}{b}=\frac{\cos A+1}{\sqrt{3} \sin B}$.
(1)求角 $A_{\text {i }}$
(2)若 $b+c=2 a$, 且 $\triangle A B C$ 外接圆的直径为 2 , 求 $\triangle A B C$ 的面积.
产品的质量是一个企业在市场中获得消费者信赖的重要因素, 某企业对出厂的每批次产品 都进行性能测试. 某检验员在某批次的产品中抽取 5 个产品进行性能测试, 现有甲、乙两种 不同的测试方案, 每个产品随机选择其中的一种进行测试, 已知选择甲方案测试合格的概率 为 $\frac{1}{2}$, 选择乙方案测试合格的概率为 $\frac{3}{4}$, 且每次测试的结果互不影㕷.
(1)若 3 个产品选择甲方案, 2 个产品选择乙方案.
(i) 求 5 个产品全部测试合格的概率;
(ii) 求 4 个产品测试合格的概率.
(2)若测试合格的产品个数的期望不小于 3, 求选捀甲方案进行测试的产品个数.
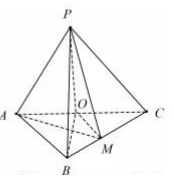
如图, 在三棱锥 $P-A B C$ 中, $A B \perp B C, A B=B C=2, P A=P B=P C=2 \sqrt{2}, O$ 为 $A C$ 的中点.
(1) 证明: $A C \perp$ 平面 $\mathrm{PBO}$;
(2)若 $M$ 为棱 $B C$ 的中点, 求二面角 $M-P A-C$ 的正弦值.
已知椭圆 $M: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点为 $F_1, F_2$, 且左焦点坐标为 $(-\sqrt{2}, 0), P$ 为 椭圆上的一个动点, $\angle F_1 P F_2$ 的最大值为 $\frac{\pi}{2}$.
(1)求椭圆 $M$ 的标准方程;
(2) 若过点 $(-2,-4)$ 的直线 $l$ 与椭圆 $M$ 交于 $A, B$ 两点, 点 $N(2,0)$, 记直线 $N A$ 的斜率为 $k_1$, 直线 NB 的斜率为 $k_2$, 证明: $\frac{1}{k_1}+\frac{1}{k_2}=1$.
已知函数 $f(x)=-a x^2+x \ln x-x$.
(1)若 $f(x)$ 有两个极值点,求实数 $a$ 的取值范围;
(2)当 $a=0$ 时, 求函数 $h(x)=f(x)-x+\frac{2}{x}$ 的零点个数.