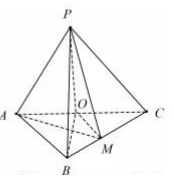
如图, 在三棱锥 $P-A B C$ 中, $A B \perp B C, A B=B C=2, P A=P B=P C=2 \sqrt{2}, O$ 为 $A C$ 的中点.
(1) 证明: $A C \perp$ 平面 $\mathrm{PBO}$;
(2)若 $M$ 为棱 $B C$ 的中点, 求二面角 $M-P A-C$ 的正弦值.
(1) 证明: $A C \perp$ 平面 $\mathrm{PBO}$;
(2)若 $M$ 为棱 $B C$ 的中点, 求二面角 $M-P A-C$ 的正弦值.
