记复数 $z$ 的共轨复数为 $z$, 若 $z(1+\mathrm{i})=2-2 \mathrm{i}$, 则 $|z|=$

已知集合 $A=\left\{x \left\lvert\, x=\frac{k \pi}{2}\right., k \in Z\right\}, B=\left\{x \left\lvert\, x=\frac{\pi}{2}+k \pi\right., k \in Z\right\}$, 则

双曲线 $\frac{x^2}{3}-y^2=1$ 的顶点到其渐近线的距离为

过 $A(-1,0), B(0,3), C(9,0)$ 三点的圆与 $y$ 轴交于 $M, N$ 两点, 则 $|M N|=$

假设甲和乙刚开始的 “日能力值” 相同, 之后甲通过学习, “日能力值” 都在前一天的基础上进步 $2 \%$, 而乙䟽于学习, “日能力值” 都在前一天的基础上退步 $1 \%$. 那么, 大约需要经过( )天, 甲的 “日能力值” 是乙的 20 倍. (参考数据: $\lg 102 \approx 2.0086, \lg 99 \approx 1.9956, \lg 2 \approx 0.3010$ )

“ $\alpha=\frac{\pi}{4}+k \pi(k \in Z)$ ” 是 “ $\frac{\sqrt{3} \cos ^2 \alpha+\sin ^2 \alpha}{\sin \alpha \cos \alpha}=\sqrt{3}+1$ ” 的

分别以锐角三角形 $A B C$ 的边 $A B, B C, A C$ 为旋转轴旋转一周后得到的几何体体积之比为 $\sqrt{3}: \sqrt{6}: 2$, 则 $\cos B=$

已知集合 $A=\left\{-\frac{1}{2},-\frac{1}{3}, \frac{1}{2}, \frac{1}{3}, 2,3\right\}$, 若 $a, b, c \in A$ 且互不相等, 则使得指数函数 $y=a^x$, 对数函数 $y=\log _b x$, 幂函数 $y=x^c$ 中至少有两个函数在 $(0,+\infty)$ 上单调递增的有序数对 $(a, b, c)$的个数是

已知向量 $\vec{a}=(1, \sqrt{3}), \vec{b}=(\cos \alpha, \sin \alpha)$, 则下列结论正确的是

已知偶函数 $f(x)$ 的定义域为 $R, f\left(\frac{1}{2} x+1\right)$ 为奇函数, 且 $f(x)$ 在 $[0,1]$ 上单调递增, 则下列结论正确的是

已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的各个顶点都在表面积为 $3 \pi$ 的球面上, 点 $P$ 为该球面上的任意一点, 则下列结论正确的是

随机变量 $X \sim N\left(\mu, \sigma^2\right)$, 若 $P(X \geqslant 70)=P(X \leqslant 90)$ 且 $P(72 \leqslant X \leqslant 80)=0.3$, 则随机变量 $X$ 的第 80 百分位数是

已知函数 $f(x)=\sin (\omega x+\varphi)(\omega>0)$ 在区间 $\left(\frac{\pi}{6}, \frac{7 \pi}{12}\right)$ 上单调, 且满足 $f\left(\frac{\pi}{6}\right)=-1, f\left(\frac{3 \pi}{4}\right)$ $=0$, 则 $\omega=$

已知直线 $l$ 与椭圆 $C: \frac{x^2}{3}+\frac{y^2}{2}=1$ 在第一象限交于 $P, Q$ 两点, $l$ 与 $x$ 轴, $y$ 轴分别交于 $M, N$两点, 且满足 $\frac{|P M|}{|Q M|}+\frac{|Q M|}{|P M|}=\frac{|P N|}{|Q N|}+\frac{|Q N|}{|P N|}$, 则 $l$ 的斜率为

已知 $0 < a < 1$, 函数 $f(x)=\frac{a e^{x-a}}{x}(x \neq 0)$.
(1) 求 $f(x)$ 的单调区间.
(2) 讨论方程 $f(x)=a$ 的根的个数.

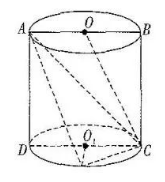
如图, 已知圆柱 $O O_1$ 的轴截面 $A B C D$ 是边长为 2 的正方形, 点 $P$ 是圆 $O_1$ 上异于点 $C, D$ 的任意一点.
(1) 若点 $D$ 到平面 $A C P$ 的距离为 $\frac{2 \sqrt{3}}{3}$, 证明: $O_1 P \perp C D$.
(2) 求 $O C$ 与平面 $A C P$ 所成角的正弦值的取值范围.

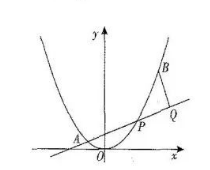
如图, 已知抛物线 $C: x^2=4 y$, 其上有定点 $A(-2,1), B(6,9)$, 动点 $P$. 在抛物线上, 且点 $P$ 位于点 $A, B$ 之间的曲线段上 (不与点 $A, B$ 重合), 过点 $B$ 作直线 $A P$ 的垂线, 垂足为 $Q$.
(1) 若点 $P$ 是 $A Q$ 的中点, 求点 $P$ 的坐标.
(2) 求 $|B Q|$ 的最大值.

某单位进行招聘面试, 已知参加面试的 $N$ 名学生全都来自 $A, B, C$ 三所学校, 其中来自 $A$ 校的学生人数为 $n(n>1)$. 该单位要求所有面试人员面试前到场, 并随机给每人安排一个面试号码 $k(k=1,2,3, \cdots, N)$, 按面试号码 $k$ 由小到大依次进行面试, 每人面试时长 5 分钟, 面试完成后自行离场.
(1) 求面试号码为 2 的学生来自 $A$ 校的概率.
(2) 若 $N=40, n=10$, 且 $B, C$ 两所学校参加面试的学生人数比为 $1: 2$, 求 $A$ 校参加面试的学生先于其他两校学生完成面试 ( $A$ 校所有参加面试的学生完成面试后, $B, C$ 两校都还有学生未完成面试) 的概率.
(3) 记随机变量 $X$ 表示最后一名 $A$ 校学生完成面试所用的时长 (从第 1 名学生开始面试到最后一名 $A$ 校学生完成面试所用的时间), $E(X)$ 是 $X$ 的数学期望, 证明: $E(X)=\frac{5 n(N+1)}{n+1}$.

数值线性代数又称矩阵计算, 是计算数学的一个重要分支, 其主要研究对象包括向量和矩阵.对于平面面量 $a=(x, y)$, 其模定义为 $|a|=\sqrt{x^2+y^2}$. 类似地, 对于 $n$ 行 $n$ 列的矩阵 $A_{n n}=$ $\left(\begin{array}{ccccc}a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & a_{n 3} & \cdots & a_{n n}\end{array}\right)$, 其模可由向量模拓展为 $A=\left(\sum_{i=1}^n \sum_{j=1}^n a_{i j}^2\right)^{\frac{1}{2}}$ (其中 $a_{i j}$ 为矩阵中第 $\mathrm{i}$行第 $j$ 列的数, $\sum$ 为求和符号), 记作 $\|A\|_F$, 我们称这样的矩阵模为弗罗贝尼乌斯范数, 例如对于矩阵 $A_{22}=\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right)=\left(\begin{array}{ll}2 & 4 \\ 3 & 5\end{array}\right)$, 其矩阵模 $A_F=\left(\sum_{i=1}^n \sum_{j=1}^n a_{i j}^2\right)^{\frac{1}{2}}=\sqrt{2^2+4^2+3^2+5^2}=3 \sqrt{6}$.弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.
(1) $\forall n \in N^*, n \geqslant 3$, 矩阵 $B_{n n}=\left(\begin{array}{ccccc}1 & 0 & 0 & \cdots & 0 \\ 0 & \sqrt{2} & 0 & \cdots & 0 \\ 0 & 0 & \sqrt{3} & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & \sqrt{n}\end{array}\right)$, 求使 $\|B\|_F>3 \sqrt{5}$ 的 $n$ 的最小值.
(2) $\forall n \in N^*, n \geqslant 3$, 矩阵 $C_{n n}=$
$$
\left(\begin{array}{ccccccc}
1 & \cos \theta & \cos \theta & \cos \theta & \ldots & \cos \theta & \cos \theta \\
0 & -\sin \theta & -\sin \theta \cos \theta & -\sin \theta \cos \theta & \ldots & -\sin \theta \cos \theta & -\sin \theta \cos \theta \\
0 & 0 & \sin ^2 \theta & \sin ^2 \theta \cos \theta & \ldots & \sin ^2 \theta \cos \theta & \sin ^2 \theta \cos \theta \\
\vdots & \vdots & \vdots & \vdots & & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & (-1)^{n-2} \sin ^{n-2} \theta & (-1)^{n-2} \sin ^{n-2} \theta \cos \theta \\
0 & 0 & 0 & 0 & \ldots & 0 & (-1)^{n-1} \sin ^{n-1} \theta
\end{array}\right) \text {, }
$$

求 $\|C\|_F$.

(3) 矩阵 $D_{n n}=\left(\begin{array}{cccccc}\ln \frac{n+2}{n+1} & 0 & 0 & 0 & \cdots & 0 \\ \ln \left(\frac{n+1}{n}\right)^{\frac{\sqrt{2}}{2}} & \ln \left(\frac{n+1}{n}\right)^{\frac{\sqrt{2}}{2}} & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & & \vdots \\ \ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} & \ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} & \ln \left(\frac{4}{3}\right)^{\frac{\sqrt{n-1}}{n-1}} & 0 & \cdots & 0 \\ \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} & \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} & \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}} & & \cdots & \ln \left(\frac{3}{2}\right)^{\frac{\sqrt{n}}{n}}\end{array}\right)$,

证明: $\forall n \in N^*, n \geqslant 3,\|D\|_F>\sqrt{\frac{n}{3 n+9}}$.