单选题 (共 8 题 ),每题只有一个选项正确
某校高一年级 18 个班参加艺术节合唱比赛, 通过简单随机抽样, 获得了 10 个班的比赛得分如下: $91,89,90,92,94,87,93,96,91,85$, 则这组数据的 $80 \%$ 分位数为
$\text{A.}$ 93
$\text{B.}$ 93.5
$\text{C.}$ 94
$\text{D.}$ 94.5
已知向量 $\vec{a}, \vec{b}$ 满足 $\vec{a} \cdot \vec{b}=1,\langle\vec{a}, \vec{b}\rangle=\frac{\pi}{3}$, 则 $|\vec{a}+\vec{b}|+2|\vec{a}-\vec{b}|$ 的最小值为
$\text{A.}$ $\sqrt{6}+2 \sqrt{2}$
$\text{B.}$ $\sqrt{6}+\sqrt{2}$
$\text{C.}$ 8
$\text{D.}$ 2
过直线 $y=x$ 上一点 $M$ 作圆 $C:(x-2)^2+y^2=1$ 的两条切线, 切点分别为 $P, Q$. 若直线 $P Q$过点 $(1,3)$, 则直线 $P Q$ 的方程为
$\text{A.}$ $5 x-y-2=0$
$\text{B.}$ $x-5 y+14=0$
$\text{C.}$ $5 x+y-8=0$
$\text{D.}$ $x+5 y-16=0$
古城赣州最早有五大城门, 分别为镇南门、百盛门、涌金门、建春门和西津门, 赣州某学校历史兴趣小组决定利用两个周日的时间对五大城门的地理位置及历史意义进行调研. 若约定: 每个城门只调研一次, 且每个周日只调研五大城门中的两大城门或三大城门, 则恰好在同一个周日调研百盛门和建春门的概率为
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{5}$
$\text{D.}$ $\frac{4}{5}$
数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 满足 $S_n+a_n=1024$, 则数列 $\left\{a_n\right\}$ 的前 $n$ 项积的最大值为
$\text{A.}$ $2^{55}$
$\text{B.}$ $2^{45}$
$\text{C.}$ $2^9$
$\text{D.}$ $2^{10}$
已知矩形 $A B C D$ 中, $A B=2, B C=1$, 将 $\triangle C B D$ 沿 $B D$ 折起至 $\square C^{\prime} B D$, 当 $C^{\prime} B$ 与 $A D$ 所成角最大时, 三棱椎 $C^{\prime}-A B D$ 的体积等于
$\text{A.}$ $\frac{\sqrt{3}}{6}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{2 \sqrt{5}}{15}$
$\text{D.}$ $\frac{2 \sqrt{5}}{5}$
已知 $\cos \left(140^{\circ}-\alpha\right)+\sin \left(110^{\circ}+\alpha\right)=\sin \left(130^{\circ}-\alpha\right)$, 求 $\tan \alpha=$
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $-\frac{\sqrt{3}}{3}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $-\sqrt{3}$
若存在 $a \in \mathbf{R}$, 使得对于任意 $x \in\left[\frac{1}{\mathrm{e}}, \mathrm{e}\right]$, 不等式 $\ln x \leq a x^2+b x \leq\left(\mathrm{e}^2-2 \mathrm{e}\right) \ln x+\mathrm{e}$ 恒成立, 则实数 $b$ 的最小值为
$\text{A.}$ $-\frac{\mathrm{e}^3+\mathrm{e}+1}{\mathrm{e}^2-1}$
$\text{B.}$ $-\frac{\mathrm{e}^2+\mathrm{e}}{\mathrm{e}^2-1}$
$\text{C.}$ $-1$
$\text{D.}$ $-\mathrm{e}$
多选题 (共 3 题 ),每题有多个选项正确
下列说法正确的是
$\text{A.}$ $\varnothing \in\{0\}$
$\text{B.}$ 集合 $\{x \mid x=2 n, n \in \mathrm{Z}\}=\left\{x \left\lvert\, \frac{x}{2} \in \mathrm{Z}\right.\right\}$
$\text{C.}$ 函数 $f(x)=\left\{\begin{array}{cc}1 & x \in \mathrm{Q} \\ 0 & x \in \complement_{\mathrm{R}} \mathrm{Q}\end{array}\right.$ 的值域为 $[0,1]$
$\text{D.}$ $f(x)=x|x|$ 在定义域内单调递增
如图, 点 $A, B, C$ 是函数 $f(x)=\sin (\omega x+\varphi)(\omega>0)$ 的图象与直线 $y=\frac{\sqrt{3}}{2}$ 相邻的三个交点,且 $|B C|-|A B|=\frac{\pi}{3}, f\left(-\frac{\pi}{12}\right)=0$, 则
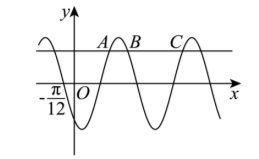
$\text{A.}$ $\omega=4$
$\text{B.}$ $f\left(\frac{9 \pi}{8}\right)=\frac{1}{2}$
$\text{C.}$ 函数 $f(x)$ 在 $\left(\frac{\pi}{3}, \frac{\pi}{2}\right)$ 上单调递减
$\text{D.}$ 若将函数 $f(x)$ 的图象沿 $x$ 轴平移 $\theta$ 个单位, 得到一个偶函数的图像, 则 $|\theta|$ 的最小值为 $\frac{\pi}{24}$
已知定义在 $(0,+\infty)$ 的函数 $f(x)$ 满足: (1)对 $\forall x \in(0,+\infty)$ 恒有 $x f^{\prime}(x)-f(x)=x$; (2)对任意的正数 $m, n$ 恒有 $f(m n)=n f(m)+m f(n)+m n$. 则下列结论中正确的有
$\text{A.}$ $f(1)=-1$
$\text{B.}$ 过点 $(\mathrm{e}, f(\mathrm{e}))$ 的切线方程 $y=x-1$
$\text{C.}$ 对 $\forall x \in(0,+\infty)$, 不等式 $f(x) \geq x-\mathrm{e}$ 恒成立
$\text{D.}$ 若 $x_0$ 为函数 $y=f(x)+x^2$ 的极值点, 则 $f\left(x_0\right)+3 x_0>0$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知复平面上一个动点 $Z$ 对应复数 $z$, 若 $|z-4 \mathrm{i}| \leq 2$, 其中 $\mathrm{i}$ 是虚数单位, 则向量 $\overrightarrow{O Z}$ 扫过的面积为
已知实数 $x, y$ 满足 $x^2-3 \ln x-y=0$, 则 $\sqrt{x^2+y^2-m x+m y+\frac{m^2}{2}}(m \in \mathrm{R})$ 的最小值为
如图, 在直角梯形 $A B C D$ 中, $A B / / C D, \angle A B C=90^{\circ}, A B=1, A C=C D=D A=2$, 动点 $M$在边 $D C$ 上 (不同于 $D$ 点), $P$ 为边 $A B$ 上任意一点, 沿 $A M$ 将 $\triangle A D M$ 翻折成 $\triangle A D^{\prime} M$, 当平面 $A D^{\prime} M$ 垂直于平面 $A B C$ 时, 线段 $P D^{\prime}$ 长度的最小值为
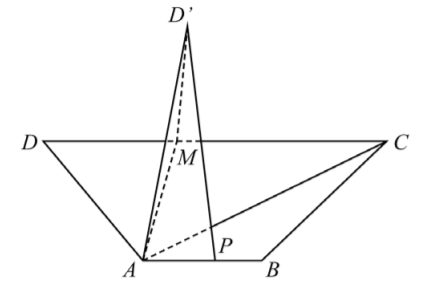
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某校举行围棋友谊赛, 甲、乙两名同学进行冠亚军决赛, 每局比赛甲获胜的概率是 $\frac{2}{3}$,乙获胜的概率是 $\frac{1}{3}$, 规定: 每一局比赛中胜方记 1 分, 负方记 0 分, 先得 3 分者获胜, 比赛结束.
(1)求进行 3 局比赛决出冠亚军的概率;
(2)若甲以 $2: 1$ 领先乙时, 记 $X$ 表示比赛结束时还需要进行的局数, 求 $X$ 的分布列及数学期望.
设函数 $f(x)=\ln x+a x+b$, 曲线 $y=f(x)$ 在点 $(1, f(1))$ 处的切线方程为 $y=6 x-3$.
(1)求 $a, b$;
(2)证明: $f(x)>-\frac{3}{5 x}$.
如图, $A B$ 是半球 $O$ 的直径, $A B=4, M, N$ 依次是底面 $A B$ 上的两个三等分点, $P$ 是半球面上一点, 且 $\angle P O N=60^{\circ}$.
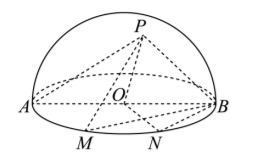
(1)证明: $P B \perp P M$;
(2)若点 $P$ 在底面圆上的射影为 $O N$ 中点, 求直线 $P M$ 与平面 $P A B$ 所成的角的正弦值.
已知双曲线 $C: \frac{x^2}{4}-y^2=1$, 点 $M(4,0)$, 经过点 $M$ 的直线交双曲线 $C$ 于不同的两点 $A 、 B$,过点 $A, B$ 分别作双曲线 $C$ 的切线, 两切线交于点 $E$. (二次曲线 $A x^2+B y^2=1$ 在曲线上某点 $\left(x_0, y_0\right)$ 处的切线方程为 $A x_0 x+B y_0 y=1$ )
(1)求证:点 $E$ 恒在一条定直线 $L$ 上;
(2)若两直线与 $L$ 交于点 $N, \overrightarrow{A N}=\lambda \overrightarrow{M A}, \overrightarrow{B N}=\mu \overrightarrow{M B}$, 求 $\lambda+\mu$ 的值;
(3)若点 $A 、 B$ 都在双曲线 $C$ 的右支上, 过点 $A 、 B$ 分别做直线 $L$ 的垂线, 垂足分别为 $P 、 Q$, 记 $\triangle A M P, \triangle B M Q$, $\triangle P M Q$ 的面积分别为 $S_1, S_2, S_3$, 问: 是否存在常数 $m$, 使得 $S_1 S_2=m S_3^2$ ? 若存在, 求出 $m$ 的值; 若不存在,请说明理由.
若各项为正的无穷数列 $\left\{a_n\right\}$ 满足: 对于 $\forall n \in \mathbf{N}^*, a_{n+1}^2-a_n^2=d$, 其中 $d$ 为非零常数, 则称数列 $\left\{a_n\right\}$ 为 $D$ 数列. 记 $b_n=a_{n+1}-a_n$.
(1)判断无穷数列 $a_n=\sqrt{n}$ 和 $a_n=2^n$ 是否是 $D$ 数列, 并说明理由;
(2)若 $\left\{a_n\right\}$ 是 $D$ 数列, 证明: 数列 $\left\{b_n\right\}$ 中存在小于 1 的项;
(3) 若 $\left\{a_n\right\}$ 是 $D$ 数列, 证明: 存在正整数 $n$, 使得 $\sum_{i=1}^n \frac{1}{a_i}>2024$.