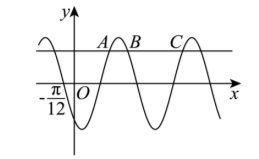
如图, 点 $A, B, C$ 是函数 $f(x)=\sin (\omega x+\varphi)(\omega>0)$ 的图象与直线 $y=\frac{\sqrt{3}}{2}$ 相邻的三个交点,且 $|B C|-|A B|=\frac{\pi}{3}, f\left(-\frac{\pi}{12}\right)=0$, 则
A
$\omega=4$
B
$f\left(\frac{9 \pi}{8}\right)=\frac{1}{2}$
C
函数 $f(x)$ 在 $\left(\frac{\pi}{3}, \frac{\pi}{2}\right)$ 上单调递减
D
若将函数 $f(x)$ 的图象沿 $x$ 轴平移 $\theta$ 个单位, 得到一个偶函数的图像, 则 $|\theta|$ 的最小值为 $\frac{\pi}{24}$
E
F