江西南昌二中2024届高三“九省联考”考后适应性测试数学试题

导出试卷

江西南昌二中2024届高三“九省联考”考后适应性测试数学试题

一、单选题（共 8 题），每题只有一个选项正确

1. 数据

6.0, 7.4, 8.0, 8.4, 8.6, 8.7, 9.0, 9.1

的 50 百分位数为

A.

8.4

B.

8.5

C.

8.6

D.

8.7

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 已知双曲线

C : y^{2} - \frac{x^{2}}{b^{2}} = 1 (b > 0)

的离心率

e < \sqrt{2}

, 则

b

的取值范围是

A.

(0, 1)

B.

(1, \sqrt{2})

C.

(1, + \infty)

D.

(\sqrt{2}, \mp \infty)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 若数列

{a_{n}}

满足

a_{2} = 11, a_{n + 1} = \frac{1}{1 - a_{n}}

, 则

a_{985} =

A.

\frac{11}{10}

B.

C.

- \frac{1}{10}

D.

\frac{10}{11}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 已知平面

α, β

, 直线

l \subset α

, 直线

m

不在平面

α

上, 下列说法正确的是

A.

若

α / / β, m / / β

, 则

l / / m

B.

若

α / / β, m ⊥ β

, 则

l ⊥ m

C.

若

l / / m, α / / β

, 则

m / / β

D.

若

l ⊥ m, m / / β

, 则

α ⊥ β

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 在某次美术专业测试中, 若甲、乙、丙三人获得优秀等级的概率分别是

0.6, 0.7

和 0.5 , 且三人的测试结果相互独立, 则测试结束后, 在甲、乙、丙三人中恰有两人没达优秀等级的前提条件下, 乙没有达优秀等级的概率为

A.

\frac{15}{29}

B.

\frac{7}{8}

C.

\frac{5}{8}

D.

\frac{17}{29}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 在平面直角坐标系中, 集合

A = {(x, y) ∣ k x - y + k = 0}

, 集合

B = {(x, y) ∣ y = k x - 1}

, 已知点

M \in A

, 点

N \in B

, 记

d

表示线段

M N

长度的最小值, 则

d

的最大值为

A.

B.

\sqrt{3}

C.

D.

\sqrt{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知函数

f (x) = \cos 2 x, g (x) = \sin x

, 则存在

θ \in (\frac{π}{6}, \frac{π}{4})

, 使得

A.

2 g (θ) = f (θ) + g (θ) \cdot f (θ)

B.

4 g (θ) \cdot f (θ) = f (θ) + 2 g (θ)

C.

2 f (θ) = g (θ) + g (θ) \cdot f (θ)

D.

f (θ) = g (θ)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知平面上两定点

A 、 B

, 则所有满足

\frac{| P A |}{| P B |} = λ (λ > 0

且

λ \neq 1)

的点

P

的轨迹是一个圆心在

A B

上,半径为

| \frac{λ}{1 - λ^{2}} | \cdot | A B |

的圆. 这个轨迹最先由古希腊数学家阿波罗尼斯发现, 故称作阿氏圆.已知棱长为 3 的正方体

A B C D - A_{1} B_{1} C_{1} D_{1}

表面上动点

P

满足

| P A | = 2 | P B |

, 则点

P

的轨迹长度为

A.

2 π

B.

\frac{4 π}{3} + \sqrt{3} π

C.

\frac{4 π}{3} + \frac{\sqrt{3} π}{2}

D.

(2 + \sqrt{3}) π

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 3 题），每题有多个选项正确

9. 已知复数

z_{0} = 1 - i, z = x + y i (x, y \in R)

, 则下列结论正确的是

A.

方程

| z - z_{0} | = 2

表示的

z

在复平面内对应点的轨迹是圆

B.

方程

| z - z_{0} | + | z - \overset{―}{z_{0}} | = 2

表示的

z

在复平面内对应点的轨迹是椭圆

C.

方程

| z - z_{0} | - | z - \overset{―}{z_{0}} | = 1

表示的

z

在复平面内对应点的轨迹是双曲线的一支

D.

方程

| z + \frac{1}{2} (z_{0} + \overset{―}{z_{0}}) | = | z - z_{0} |

表示的

z

在复平面内对应点的轨迹是抛物线

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 已知

θ

为锐角, 则下列说法错误的是

A.

满足

\tan θ = \cos θ + \sin θ

的

θ

值有且仅有一个

B.

满足

\sin θ, \tan θ, \cos θ

成等比数列的

θ

值有且仅有一个

C.

\sin θ, \cos θ, \tan θ

三者可以以任意顺序构成等差数列

D.

存在

θ

使得

\tan θ - \sin θ, \cos θ - \sin θ, \cos θ - \tan θ

成等比数列

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知无穷数列

{a_{n}}, a_{1} = 1

. 性质

s : \forall m, n \in N^{*}, a_{m + n} > a_{m} + a_{n}

, 性质

t : \forall m, n \in N^{*}

2 \leq m < n, a_{m - 1} + a_{n + 1} > a_{m} + a_{n}

, 下列说法中正确的有

A.

若

a_{n} = 3 - 2 n

, 则

{a_{n}}

具有性质

s

B.

若

a_{n} = n^{2}

, 则

{a_{n}}

具有性质

t

C.

若

{a_{n}}

具有性质

s

, 则

a_{n} \geq n

D.

若等比数列

{a_{n}}

既满足性质

s

又满足性质

t

, 则其公比的取值范围为

(2, + \infty)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 3 题），请把答案直接填写在答题纸上

12. 已知

p : - 3 \leq x \leq 1, q : x \leq a

(

a

为实数). 若

q

的一个充分不必要条件是

p

, 则实数

a

的取值范围是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 各棱长均为 1 且底面为正方形的平行六面体

A B C D - A_{1} B_{1} C_{1} D_{1}

, 满足

∠ A_{1} A B = ∠ A_{1} A D = 60^{\circ}

, 则

| A C_{1} | =

; 此平行六面体的体积为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 已知定义在

R

上的增函数

f (x)

满足对任意的

x_{1}, x_{2} \in R

都有

f (x_{1} + x_{2}) = f (x_{1}) f (x_{2})

, 且

f (3) = 8

, 函数

g (x)

满足

g (x) + g (4 - x) = 4, g (6 - x) = g (x)

, 且当

x \in [2, 3]

时

g (x) = f (x - 1)

. 若

g (x)

在

[0, 100]

上取得最大值的

x

值依次为

x_{1}, x_{2}, \dots, x_{k}

, 取得最小值的

x

值依次为

x_{1}^{'}, x_{2}^{'}, \dots

x_{n}^{'}

, 则

\sum_{i = 1}^{k} [x_{i} + g (x_{i})] + \sum_{i = 1}^{n} [x_{i}^{'} + g (x_{i}^{'})] =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

四、解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

15. 已知函数

f (x) = \ln x + \frac{a}{2} x^{2} - (a + 1) x, g (x) = - a x^{2} + (a + 1) x

.
(1) 讨论函数

f (x)

的单调性;
(2) 若

f (x) + g (x) \leq 0

恒成立, 求

a

的取值范围.

查看分享下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

16. 有两个盒子, 其中 1 号盒子中有 3 个红球, 2 个白球; 2 号盒子中有 6 个红球, 4 个白球. 现按照如下规则摸球. 从两个盒子中任意选择一个盒子, 再从盒中随机摸出 2 个球, 摸球的结果是一红一白.
(1) 你认为较大可能选择的是哪个盒子?请做出你的判断, 并说明理由;
(2) 如果你根据 (1) 中的判断, 面对相同的情境, 作出了 5 次同样的判断, 记判断正确的次数为

X

, 求

X

的数学期望 (实际选择的盒子与你认为较大可能选择的盒子相同时, 即为判断正确).

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 如图 1, 已知正三角形

A B C

边长为 4 , 其中

\vec{A D} = 3 \vec{D B}, \vec{A E} = 3 \vec{E C}

, 现沿着

D E

翻折, 将点

A

翻折到点

A^{'}

处, 使得平面

A^{'} B C ⊥

平面

D B C, M

为

A^{'} C

中点, 如图 2.

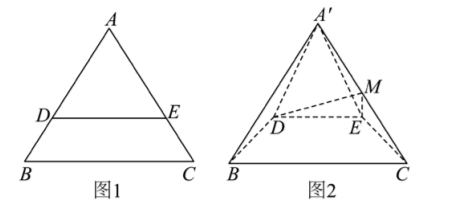
(1) 求异面直线

A^{'} D

与

E M

所成角的余弦值;
(2) 求平面

A^{'} B C

与平面

D E M

夹角的余弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 在平面直角坐标系

x O y

中, 已知抛物线

C : y^{2} = 2 p x (p > 0)

和点

R (4, 5)

. 点

P

在

C

上, 且

\vec{O P} = \frac{4}{5} \vec{O R}

.
(1) 求

C

的方程;
(2) 若过点

R

作两条直线

l_{1}

与

l_{2}, l_{1}

与

C

相交于

A, B

两点,

l_{2}

与

C

相交于

E, D

两点, 线段

A B

和

E D

中点的连线的斜率为

k

, 直线

A B, E D, A D, B E

的斜率分别为

k_{1}, k_{2}, k_{3}, k_{4}

, 证明:

\frac{1}{k_{1}} + \frac{1}{k_{2}} = \frac{1}{k_{3}} + \frac{1}{k_{4}}

, 且

\frac{1}{k_{3}} + \frac{1}{k_{4}} - \frac{1}{k}

为定值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 若存在

x_{0} \in D

使得

f (x) \leq f (x_{0})

对任意

x \in D

恒成立, 则称

x_{0}

为函数

f (x)

在

D

上的最大值点, 记函数

f (x)

在

D

上的所有最大值点所构成的集合为

M

(1) 若

f (x) = - x^{2} + 2 x + 1, D = R

, 求集合

M

；
(2) 若

f (x) = \frac{(2^{x} - x) x}{4^{x}}, D = R

, 求集合

M

;
(3) 设

a

为大于 1 的常数, 若

f (x) = x + a \sin x, D = [0, b]

, 证明, 若集合

M

中有且仅有两个元素, 则所有满足条件的

b

从小到大排列构成一个等差数列.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。