如图 1, 已知正三角形 $A B C$ 边长为 4 , 其中 $\overrightarrow{A D}=3 \overrightarrow{D B}, \overrightarrow{A E}=3 \overrightarrow{E C}$, 现沿着 $D E$ 翻折, 将点 $\mathrm{A}$ 翻折到点 $A^{\prime}$ 处, 使得平面 $A^{\prime} B C \perp$ 平面 $D B C, M$ 为 $A^{\prime} C$ 中点, 如图 2.
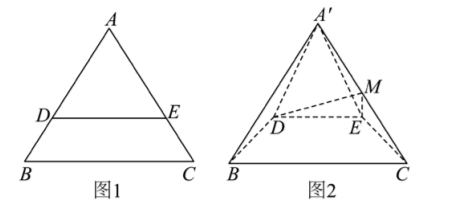
(1) 求异面直线 $A^{\prime} D$ 与 $E M$ 所成角的余弦值;
(2) 求平面 $A^{\prime} B C$ 与平面 $D E M$ 夹角的余弦值.