单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $M=\{x \mid x>1\}, N=\left\{x \mid \log _2 x>1\right\}$, 则
$\text{A.}$ $M \cap N=\{x \mid x>1\}$
$\text{B.}$ $M \cup N=\{x \mid x>1\}$
$\text{C.}$ $C_M N=\{x \mid 1 < x < 2\}$
$\text{D.}$ $M=N$
复数 $\mathrm{z}$ 满足 $\left|\frac{z}{1+i}\right|^2=z(2-i)$, $\mathrm{i}$ 为虚数单位, 则 $|z|=$
$\text{A.}$ 1
$\text{B.}$ 1 或 $3 \sqrt{2}$
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ 0 或 $2 \sqrt{5}$
已知向量 $\mid \vec{a}=(4,2)$, 向量 $\vec{b}=(x,-1)$, 若 $\vec{a} / / \vec{b}$, 则 $|\vec{b}|=$
$\text{A.}$ $\sqrt{5}$
$\text{B.}$ $5$
$\text{C.}$ $\frac{\sqrt{5}}{2}$
$\text{D.}$ $\frac{5}{4}$
已知数列 $\left\{\mathrm{a}_{\mathrm{n}}\right\}$ 满足 $\dfrac{a_{n+1}-a_n}{\left(1+a_1^2\right)\left(1+a_2^2\right) \mathrm{...}\left(1+a_n^2\right)}=0 \quad\left(\mathrm{n} \in \mathrm{N}^*\right)$, 则
$\text{A.}$ $a_{2021}>a_1$
$\text{B.}$ $\mathrm{a}_{2021} < \mathrm{a}_1$
$\text{C.}$ 数列 $\left\{\mathrm{a}_{\mathrm{n}}\right\}$ 是等差数列
$\text{D.}$ 数列 $\left\{a_n\right\}$ 是等比数列
抛物线 $y^2=2 p x(p>0)$ 的焦点到直线 $y=x+1$ 的距离为 $\sqrt{2}$, 则 $p=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ $2 \sqrt{2}$
$\text{D.}$ 4
执行如图所示的程序框图,输出的结果是
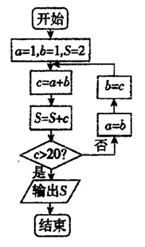
$\text{A.}$ 56
$\text{B.}$ 54
$\text{C.}$ 36
$\text{D.}$ 64
四面体 $A B C D$ 中, $A B=C D=3$, 其余棱长均为 $4, E, F$ 分别为 $A B, C D$ 上的点 (不含端点), 则
$\text{A.}$ 不存在 $E$, 使得 $E F \perp C D$
$\text{B.}$ 存在 $E$, 使得 $D E \perp C D$
$\text{C.}$ 存在 $E$, 使得 $D E \perp$ 平面 $A B C$
$\text{D.}$ 存在 $E, F$, 使得平面 $C D E \perp$ 平面 $A B F$
设数列 $\left\{\mathrm{a}_{\mathrm{n}}\right\}$ 的前 $\mathrm{n}$ 项和为 $\mathrm{S}_{\mathrm{n}}$, 若 $a_n=\frac{1}{\sqrt{n+1}+\sqrt{n}}$, 则 $\mathrm{S}_{99}=$
$\text{A.}$ 7
$\text{B.}$ 8
$\text{C.}$ 9
$\text{D.}$ 10
已知圆柱的上、下底面的中心分别为 $O, O^{\prime}$, 过直线 $O O^{\prime}$ 的平面截该圆柱所得的面是面积为 8 的正方 形, 则该圆柱的表面积为
$\text{A.}$ $12 \sqrt{2} \pi$
$\text{B.}$ $12 \pi$
$\text{C.}$ $8 \sqrt{2} \pi$
$\text{D.}$ $10 \pi$
某公司为了促进技术部门之间良好的竞争风气,公司决定进行一次信息化技术比赛,三个技术部门分别为麒麟部,龙吟部,鹰隼部,比赛规则如下:①每场比赛有两个部门参加,并决出胜负;②每场比赛获胜的部门与未参加此场比赛的部门进行下一场的比赛;③在比赛中,若有一个部门首先获胜两场,则本次比赛结束,该部门就获得此次信息化比赛的“优胜部门”.已知在每场比赛中,麒麟部胜龙吟部的概率为 ,麒麟部胜鹰隼部的概率为3/5,龙吟部胜鹰隼部的概率为1/2.当麒麟部与龙吟部进行首场比赛时,麒麟部获得“优胜部门”的概率是
$\text{A.}$ $\frac{4}{45}$
$\text{B.}$ $\frac{2}{9}$
$\text{C.}$ $\frac{4}{15}$
$\text{D.}$ $\frac{13}{45}$
已知 $F_1$ 是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点, 点 $P$ 在双曲线上, 直线 $P F_1$ 与 $x$ 轴垂直, 且 $\left|P F_1\right|=a$, 那么双曲线的离心率是
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ 2
$\text{D.}$ 3
已知函数 $f(x)=\left\{\begin{array}{c}x, x>0 \\ e^{2 x}, x \leq 0^{\prime}\end{array}, g(x)=-x^2+2 x\right.$ (其中 $e$ 是自然对数的底数), 若关于 $x$ 的方程 $g(f(x))-m=0$ 恰有三个不等实根 $x_1, x_2, x_3$, 且 $x_1 < x_2 < x_3$, 则 $x_2-2 x_1-2 x_3$ 的最小值为
$\text{A.}$ $\ln 3-3$
$\text{B.}$ $\frac{3}{2}-\ln 2$
$\text{C.}$ $\ln 2-3$
$\text{D.}$ $-1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知甲、乙两名篮球运动员投篮投中的概率分别为0.5和0.8,且甲、乙两人投篮的结果互不影响.若甲、乙两人各投篮一次,则至少有一人投中的概率为
已知椭圆的中心在坐标原点, 右焦点与圆 $x^2+m y^2-6 m x-7=0$ 的圆心重合, 长轴长等于圆的直 径, 那么短轴长等于
已知函数 $f(x)=\sin \left(\omega x+\frac{\pi}{4}\right)(x \in \mathbf{R}, \omega>0)$ 的最小焉周期为 $\pi$, 将 $y=f(x)$ 的图象向左平移 $\phi$ $(\varphi>0)$ 个单位长度, 所得函数 $y=g(x)$ 为偶函数时, 则 $\phi$ 的最小值是
函数 $f(x)=x^2-\frac{a}{2} \ln x-\frac{x}{2}(a \in \mathbf{R})$ 在 $\left[\frac{1}{16}, 1\right]$ 内不存在极值点, 则 $\mathrm{a}$ 的取值范围是
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 的内角 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 的对边分别为 $a, b, c, \frac{\sin B}{2 b}=\frac{\cos C}{c}$.
(1) 求 $\frac{\sin C+2 \cos C}{2 \sin C-\cos C}$ 的值;
(2) 若 $c=2 \sqrt{5}, \triangle A B C$ 的面积为 5 , 求 $\triangle A B C$ 的周长.
如图, $C$ 是以 $A B$ 为直径的圆 $O$ 上异于 $A, B$ 的点, 平面 $P A C$ 平面 $A B C, \triangle P A C$ 中, $P A=P C$ $=A C=2, B C=4, E, F$ 分别是 $P C, P B$ 的中点.
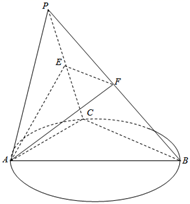
|(1) 求证: $B C \perp$ 平面 $P A C$;
(2) 记平面 $A E F$ 与平面 $A B C$ 的交线为直线 $l$, 点 $Q$ 为直线 $l$ 上动点. 求直线 $P Q$ 与平面 $A E F$ 所 成的角的取值范围.
在 2020年的新冠肺炎疫情影响下,国内国际经济形势呈现出前所未有的格局.某企业统计了2020 年前 5个月份企业的利润,如下表所示:
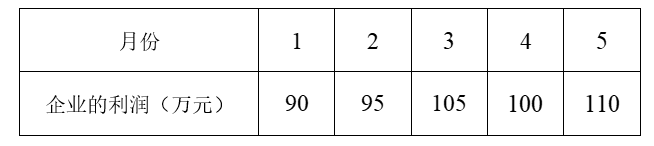
(1) 根据所给的数据建立该企业所获得的利润 $y$ (万元) 关于月份 $x$ 的回归直线方程 $\hat{y}=\hat{b} x+\hat{a}$, 并预测 2020 年 12 月份该企业所获得的利润;
(2) 企业产品的质量是企业的生命, 该企业为了生产优质的产品投放市场, 对于生产的每一件产品 必须要经过四个环节的质量检查, 若每个环节中出现不合格产品立即进行修复, 且每个环节是相互 独立的, 前三个环节中生产的产品合格的概率为 $\frac{1}{2}$, 每个环节中不合格产品所需要的修复费用均为 100 元, 第四个环节中产品合格的概率为 $\frac{3}{4}$, 不合格产品需要的修复费用为 50 元, 设每件产品修复 的费用为 $\xi$ 元, 写出 $\xi$ 的分布列, 并求出每件产品需要修复的平均费用.
参考公式: 回归直线方程 $\hat{y}=\hat{b} x+\hat{a}$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b}=\frac{\sum_{i=1}^n x_i y_i-n \overline{x y}}{\sum_{i=1}^n x_i^2-n \bar{x}^2}$, $\hat{a}=\bar{y}-\hat{b} \bar{x}, \bar{x}, \bar{y}$ 为样本数据的平均值.
已知等轴双曲线的顶点 $F_1(-2,0), F_2(2,0)$ 分别是椭圆 $C$ 的左、右焦点, 且 $x=\frac{4 \sqrt{3}}{3}$ 是粗圆与双 曲线某个交点的横坐标.
(1) 求椭圆 $C$ 的方程;
(2) 设直线 $l$ 与椭圆 $C$ 相交于 $A, B$ 两点, 以线段 $A B$ 为直径的圆过椭圆的上顶点 $M$, 求证: 直 线 $l$ 恒过定点.
已知函数 $f(x)=\frac{1}{2} x^2-a x$.
(1) 若 $\mathrm{g}(x)=f(x)-x+a \ln x$, 讨论 $\mathrm{g}(x)$ 的单调性;
(2) 已知 $h(x)=2 f(x)-x \ln x-4 a+2$, 若方程 $h(x)=0$ 在 $\left.\frac{1}{2},+\infty\right)$ 有且只有两个解, 求实数 $a$ 的取 值范围.
在直角坐标系 $x O y$ 中, 曲线 $C_1$ 的参数方程为 $\left\{\begin{array}{l}x=\cos ^k t, \\ y=\sin ^k t\end{array}\right.$ ( $t$ 为参数). 以坐标原点为极点, $x$ 轴正半 轴为极轴建立极坐标系, 曲线 $C_2$ 的极坐标方程为 $4 \rho \cos \theta-16 \rho \sin \theta+3=0$.
(1) 当 $k=1$ 时, $C_1$ 是什么曲线?
(2) 当 $k=4$ 时, 求 $C_1$ 与 $C_2$ 的公共点的直角坐标.
已知 $f(x)=|x-a| x+|x-2|(x-a)$.
(1) 当 $a=1$ 时, 求不等式 $f(x) < 0$ 的解集;
(2) 若 $x \in(-\infty, 1)$ 时, $f(x) < 0$, 求 $a$ 的取值范围.