单选题 （共 12 题 ），每题只有一个选项正确
设全集 $U=\{-1,0,1,2,3\}$, 集合 $A=\{-1,0,1\}, B=\{-1,1\}$, 则 $C_U(A \cap B)=$
$\text{A.}$ $\{2\}$
$\text{B.}$ $\{2,3\}$
$\text{C.}$ $\{0,2,3\}$
$\text{D.}$ $\{0,1,2,3\}$
设复数 $z=\frac{10}{3-\mathrm{i}}+2 \mathrm{i}$, 则 $|z|=$
$\text{A.}$ $3 \sqrt{2}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $\sqrt{10}$
已知向量 $a=(m+4, m), b=(3,1)$, 且 $a / / b$, 则 $m=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
下图是我国跨境电商在 2016-2022 年的交易规模与增速表, 由图可以知道下列结论正确的是
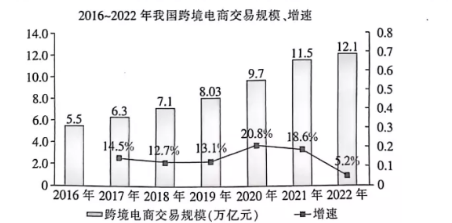
$\text{A.}$ 这 7 年我国跨境电商交易规模的平均数为 $8.0$ 万亿元
$\text{B.}$ 这 7 年我国跨境电商交易规模的增速越来越大
$\text{C.}$ 这 7 年我国跨境电商交易规模的极差为 $7.6$ 万亿元
$\text{D.}$ 图中我国跨境电商交易规模的 6 个增速的中位数为 $13.8 \%$
设函数 $f(x)=2 \ln x-\frac{1}{2} x^2+x$ 的图象在 $x=1$ 处的切线为 $l$, 则 $l$ 在 $x$ 轴上的截距为
$\text{A.}$ $-\frac{3}{4}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ $-\frac{3}{2}$.
函数 $f(x)=\frac{3^x \cos 6 x}{3^{2 x}-1}$ 的图象大致为
$\text{A.}$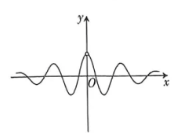 
$\text{B.}$ 
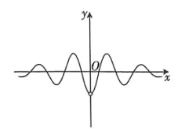$\text{C.}$ 
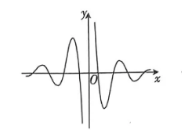$\text{D.}$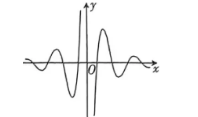 
将函数 $f(x)=2 \sin \left(2 x-\frac{\pi}{6}\right)$ 的图象向左平移 $\frac{\pi}{4}$ 个单位长度, 得到函数 $g(x)$ 的图象, 下列说 法正确的是
$\text{A.}$ $g(x)$ 为奇函数
$\text{B.}$ $g(x)$ 在 $\left[0, \frac{\pi}{3}\right]$ 上单调递减
$\text{C.}$ $g(x)$ 在 $\left[-\frac{\pi}{6}, \frac{\pi}{6}\right]$ 上的值域为 $[0, \sqrt{3}]$
$\text{D.}$ 点 $\left(-\frac{\pi}{6}, 0\right)$ 是 $g(x)$ 图象的一个对称中心
设椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的半焦距为 $c$, 若 $a-c=4, b=6$, 则 $C$ 的离心率为
$\text{A.}$ $\frac{5}{12}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{5}{13}$
$\text{D.}$ $\frac{12}{13}$
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $E$ 为 $B C$ 的中点, 则异面直线 $A_1 C$ 与 $B_1 E$ 所成角的余弦值为
$\text{A.}$ $\frac{\sqrt{10}}{5}$
$\text{B.}$ $\frac{\sqrt{15}}{5}$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{2 \sqrt{5}}{5}$
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $S_3=-27, a_4=5 a_6$, 且 $S_m>0$, 则 $m$ 的最小值为
$\text{A.}$ 11
$\text{B.}$ 12
$\text{C.}$ 13
$\text{D.}$ 14
如图, 青铜器的上半部分可以近似看作圆柱体, 下半部分可以近似看作两个圆台的组合体, 已知 $A B=9 \mathrm{~cm}, C D=3 \mathrm{~cm}$, 则该青铜器的表面积为 (假设上、下底面圆是封闭的)
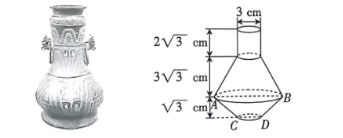
$\text{A.}$ $\frac{(36 \sqrt{3}+81) \pi}{2} \mathrm{~cm}^2$
$\text{B.}$ $(18 \sqrt{3}+58) \pi \mathrm{cm}^2$
$\text{C.}$ $\frac{(24 \sqrt{3}+81) \pi}{2} \mathrm{~cm}^2$
$\text{D.}$ $(18 \sqrt{3}+36) \pi \mathrm{cm}^2$
定义函数 $\min \{f(x), g(x)\}=\left\{\begin{array}{l}f(x), f(x) \leqslant g(x), \\ g(x), f(x)>g(x),\end{array}, \quad\right.$ (x) $\min \left\{|x|-1, x^2-2 a x+a+2\right\}$, 若 $h(x)=0$ 至少有 3 个不同的解, 则实数 $a$ 的取值范围是
$\text{A.}$ $[1,2]$
$\text{B.}$ $[2,3]$
$\text{C.}$ $[3,4]$
$\text{D.}$ $[4,5]$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
设 $x, y$ 满足约束条件 $\left\{\begin{array}{l}3 x-2 y-5 \leqslant 0, \\ x \geqslant 1, \\ y \leqslant 2,\end{array}\right.$ 则 $z=-2 x+y$ 的最小值为
已知函数 $f(x)=(x-1)(3-x)$, 在 $[0,5]$ 上任取一个实数 $x$, 使得 $f(x) \geqslant 0$ 的概率为
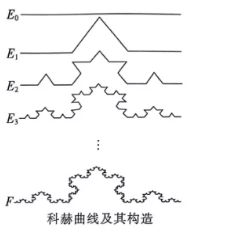
1904 年, 瑞典科学家海里格 ・冯 ・科赫引人一条曲线一一科赫曲线,曲线是这样构造的: (1)作一直线段 $E_0$; (2)将直线段 $E_0$ 三等分, 以中间三分之一线段为底作一个等边三角形, 并擦去等边三角形 的底, 得到由四条线段构成的折线图 $E_1$; (3)对 $E_1$ 的每条线段同样 用等边三角形的两边替代原线段的三分之一线段,得到折线图 $E_2 $ (4)无限重复上述过程,依次得到 $E_3, E_4, \cdots \cdots$, ,最后得到一条复杂曲线 $F$ 即称为科赫曲线,
若线段 $E_0$ 的长度为 1 米, 则 $E_n$ 的长度为 （ ）
若$E_n \ge 10000$ ,则正整数$n$的最小值为 （ ）
已知抛物线 $C: x^2=2 y$, 直线 $l$ 与抛物线 $C$ 交于 $A, B$ 两点, 过 $A, B$ 分别作抛物线 $C$ 的切线 $l_1, l_2$ 若 $l_1 \perp l_2$, 且 $l_1$ 与 $l_2$ 交于点 $M$, 则 $\triangle M A B$ 的面积的最小值为
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
$\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $b \cos C+c \cos B=\frac{\sqrt{3}}{3} a \tan C$.
(1) 求角 $C$;
(2) 若 $b=2 a, \triangle A B C$ 的面积为 $2 \sqrt{3}$, 求 $c$.
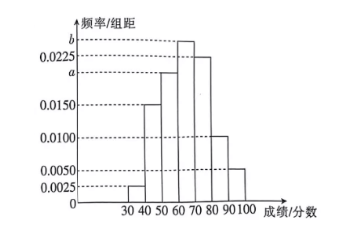
某校近期举行了 “2022 年新闻时事知识竞赛”, 现在随机抽查参赛的 200 名学生的得分 (满 分 100 分), 按照 $[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]$ 制作成如 图所示的频率分布直方图, 已知 $0.015, a, b$ 成等差数列.
(1)求出 $a, b$ 的值,并计算参赛得分在 $[60,70)$ 的学生人数;
(2)学校为进一步了解学生对新闻时事获取的途径, 准备从得分在 $[30,40)$ 与 $[90,100]$ 的学生中按分层抽样的方法抽出 6 名学生,然后从中再选出 $2$ 名学生交流新闻时事获取的途径, 求这 2人中恰有 1 人的得分在 $[30,40)$ 内的概率.
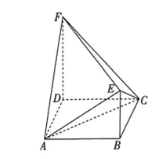
如图, 四边形 $A B C D$ 是菱形, $\angle B A D=60^{\circ}, E B \perp$ 平面 $A B C D, F D / / E B$, $F D=A B=4 E B=4$.
(1)证明: $A C \perp E F$.
(2)求点 $D$ 到平面 $C E F$ 的距离.
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的离心率为 $\sqrt{2}$, 且点 $A(2,1)$ 在 $C$ 上.
(1) 求双曲线 $C$ 的方程;
(2) 若点 $M, N$ 在双曲线 $C$ 上, 且 $A M \perp A N$, 直线 $M N$ 不与 $y$ 轴平行, 证明: 直线 $M N$ 的斜 率 $k$ 为定值.
已知函数 $f(x)=\frac{a}{3} x^3-a x-x \ln x$.
(1) 若 $f(x)$ 的导函数为 $g(x)$, 讨论 $g(x)$ 的单调性;
(2) 若 $f(x)-\frac{a x^3}{3}+(x-a) \ln x+x \mathrm{e}^x \geqslant 0$ 恒成立, 求实数 $a$ 的取值范围.
选修 4-4:坐标系与参数方程
在直角坐标系 $x O y$ 中, 曲线 $C$ 的参数方程为 $\left\{\begin{array}{l}x=2 \cos \theta, \\ y=\sqrt{3} \sin \theta\end{array}\right.$ ( $\theta$ 为参数), 以坐标原点 $O$ 为极点, $x$ 轴的正半轴为极轴建立极坐标系.
(1) 写出曲线 $C$ 的极坐标方程;
(2)已知 $A, B$ 是曲线 $C$ 上的两点, 且 $\angle A O B=\frac{\pi}{4}$, 求 $\frac{1}{|O A|^2}+\frac{1}{|O B|^2}$ 的最大值.
选修 4-5:不等式选讲
已知函数 $f(x)=|x+1|+|x-1|$.
(1) 求不等式 $f(x) \leqslant 6$ 的解集;
(2) 若 $x \in[0,2]$, 不等式 $f(x) \leqslant|x-a|$ 恒成立, 求实数 $a$ 的取值范围.