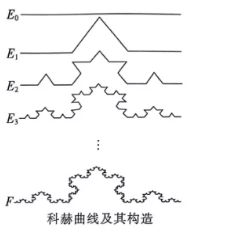
1904 年, 瑞典科学家海里格 ・冯 ・科赫引人一条曲线一一科赫曲线,曲线是这样构造的: (1)作一直线段 $E_0$; (2)将直线段 $E_0$ 三等分, 以中间三分之一线段为底作一个等边三角形, 并擦去等边三角形 的底, 得到由四条线段构成的折线图 $E_1$; (3)对 $E_1$ 的每条线段同样 用等边三角形的两边替代原线段的三分之一线段,得到折线图 $E_2 $ (4)无限重复上述过程,依次得到 $E_3, E_4, \cdots \cdots$, ,最后得到一条复杂曲线 $F$ 即称为科赫曲线,
若线段 $E_0$ 的长度为 1 米, 则 $E_n$ 的长度为 ( )
若$E_n \ge 10000$ ,则正整数$n$的最小值为 ( )
若线段 $E_0$ 的长度为 1 米, 则 $E_n$ 的长度为 ( )
若$E_n \ge 10000$ ,则正整数$n$的最小值为 ( )
