单选题 （共 24 题 ），每题只有一个选项正确
设 $x, y>1, z>0$ ，若 $z^2=x \cdot y$ ，则 $\frac{1 g z}{21 g x}+\frac{1 g z}{41 g y}$ 的最小值为（）
$\text{A.}$ $\frac{3}{8}+\frac{\sqrt{2}}{4}$
$\text{B.}$ $2 \sqrt{2}+\frac{1}{2}$
$\text{C.}$ $\frac{4}{3}+\frac{\sqrt{2}}{4}$
$\text{D.}$ $2 \sqrt{2}$
下列选项正确的是（ ）
$\text{A.}$ $\frac{a}{b}+\frac{b}{a} \geqslant 2$
$\text{B.}$ $x +\frac{4}{ x } \geqslant 4$
$\text{C.}$ $\sin ^2 \alpha+\frac{2}{\sin ^2 \alpha}$ 的最小值为 $2 \sqrt{2}$
$\text{D.}$ $x^2+\frac{1}{x^2+2}$ 的最小值为 $\frac{1}{2}$
若 $a>0, b>0$ ，且 $a+b=1$ ，则下列说法正确的是（ ）
$\text{A.}$ $\frac{1}{a}+\frac{2}{b+1} \geqslant \frac{3}{2}+\sqrt{2}$
$\text{B.}$ $a^2+b^2 \leqslant \frac{1}{2}$
$\text{C.}$ $\frac{3}{ a +1}- b >2 \sqrt{3}-2$
$\text{D.}$ $2 a ^2+ b >\frac{7}{8}$
已知 $a>0, b>0$ ，若 $\sqrt{2}$ 是 $2^a$ 与 $2^b$ 的等比中项，则 $\frac{1}{a}+\frac{1}{b}$ 的最小值是（ ）
$\text{A.}$ 8
$\text{B.}$ 4
$\text{C.}$ 3
$\text{D.}$ 2
已知 $a>2$ ，则 $2 a +\frac{8}{ a -2}$ 的最小值是（ ）
$\text{A.}$ 6
$\text{B.}$ 8
$\text{C.}$ 10
$\text{D.}$ 12
设实数 $x, y$ 满足 $x+y=1, y>0, x>0$ ，则 $\frac{2}{| x |}+\frac{| x |}{ y }$ 的最小值为 $(\quad)$
$\text{A.}$ $2 \sqrt{2}-2$
$\text{B.}$ $2 \sqrt{2}+2$
$\text{C.}$ $\sqrt{2}-1$
$\text{D.}$ $\sqrt{2}+1$
若 $a>0, b>1$ ，且 $a^2\left(b+4 b^2+2 a^2\right)=8-2 b^3$ ，则（ ）
$\text{A.}$ $8 a^2+4 b^2+3 b$ 的最小值为 $8 \sqrt{3}$
$\text{B.}$ $8 a^2+4 b^2+3 b$ 的最小值为 $8 \sqrt{2}$
$\text{C.}$ $8 a^2+4 b^2+3 b$ 的最小值为 16
$\text{D.}$ $8 a^2+4 b^2+3 b$ 没有最小值
已知 $a>1$ ，则 $a+\frac{16}{a-1}$ 的最小值为（ ）
$\text{A.}$ 8
$\text{B.}$ 9
$\text{C.}$ 10
$\text{D.}$ 11
《几何原本》第二卷中的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多代数的定理都能够通过图形实现证明，并称之为无字证明．现有如图所示的图形，点 $F$ 在半圆 $O$ 上，且 $O F \perp A B$ ，点 $C$ 在直径 $A B$ 上运动．作 $C D \perp A B$ 交半圆 $O$ 于点 $D$ ．设 $A C=a$ ， $B C=b$ ，则由 $F C \geqslant C D$ 可以直接证明的不等式为
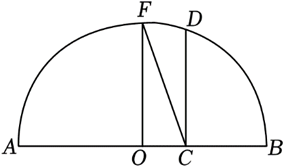
$\text{A.}$ $\frac{a+b}{2} \geqslant \sqrt{a b}(a>0, b>0)$
$\text{B.}$ $a^2+b^2 \geqslant 2 a b(a>0, \quad b>0)$
$\text{C.}$ $\frac{2 a b}{a+b} \leqslant \sqrt{\frac{a^2+b^2}{2}}(a>0, b>0)$
$\text{D.}$ $\sqrt{a b} \leqslant \sqrt{\frac{a^2+b^2}{2}}(a>0, b>0)$
已知 $a, b$ 均为正数，且 $\frac{1}{ a +1}+\frac{2}{b-2}=\frac{1}{2}$ ，则 $2 a+b$ 的最小值为（ ）
$\text{A.}$ 8
$\text{B.}$ 16
$\text{C.}$ 24
$\text{D.}$ 32
若实数 $x, y$ 满足 $x^2+4 y^2-x y=3$ ，则（ ）成立．
$\text{A.}$ $x y \geqslant 1$
$\text{B.}$ $x^2+4 y^2 \leqslant 4$
$\text{C.}$ $x +2 y \geqslant-\sqrt{2}$
$\text{D.}$ $x +2 y \leqslant \sqrt{2}$ ．
如图，在 $\triangle A B C$ 中，$M$ 为线段 $B C$ 的中点，$G$ 为线段 $A M$ 上一点且 $\overrightarrow{ AG }=2 \overrightarrow{ GM }$ ，过点 $G$ 的直线分别交直线 $A B, ~ A C$ 于 $P, ~ Q$ 两点， $\overrightarrow{ AB }= x \overrightarrow{ AP }( x >0), \overrightarrow{ AC }= y \overrightarrow{ AQ }( y >0)$ ，则 $\frac{1}{ x }+\frac{1}{ y +1}$的最小值为
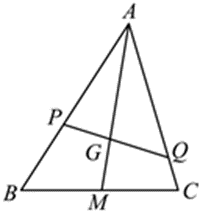
$\text{A.}$ $\frac{3}{4}$
$\text{B.}$ 1
$\text{C.}$ $\frac{4}{3}$
$\text{D.}$ 4
已知 $a>0, b>0,9$ 是 $3^a$ 与 $27^b$ 的等比中项，则 $\frac{a^2+2}{a}+\frac{3 b^2+1}{b}$ 的最小值为（ ）
$\text{A.}$ $9+2 \sqrt{6}$
$\text{B.}$ $\frac{21+2 \sqrt{6}}{4}$
$\text{C.}$ 7
$\text{D.}$ $\frac{14+2 \sqrt{6}}{3}$
若集合 $A =\left\{ x \left\lvert\, \frac{ x +1}{ x -2} \leqslant 0\right.\right\}, B =\left\{ x \mid \log _2 x \leqslant 1\right\}$ ，则 $A \cap B=$
$\text{A.}$ $[-1,2]$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $[0,2]$
$\text{D.}$ $(0,2)$
在 $R$ 上定义运算 $\otimes: x \otimes y=\frac{ x }{2-y}$ ，若关于 $x$ 的不等式 $(x-a) \otimes(x-1-a) \geqslant 0$ 的解集是集合 $\{x \mid-2 < x \leqslant 4\}$ 的子集，则实数 $a$ 的取值范围为（ ）
$\text{A.}$ $-2 < a < 1$
$\text{B.}$ $-2 \leqslant a < 1$
$\text{C.}$ $-2 < a \leqslant 1$
$\text{D.}$ $-2 \leqslant a \leqslant 1$
设 $x \in R$ ，则＂ $\log _2 x < 1$＂是＂$x^2+x-6 < 0$＂的（ ）
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知 $\log _{ a } \frac{1}{4} < 1,\left(\frac{1}{3}\right)^{ a } < 1, a ^{\frac{1}{2}} < 1$ ，则实数 $a$ 的取值范围为
$\text{A.}$ $\left(\frac{1}{3}, 1\right)$
$\text{B.}$ $\left(0, \frac{1}{4}\right) \cup(1,+\infty)$
$\text{C.}$ $\left(\frac{1}{4}, 1\right)$
$\text{D.}$ $\left(0, \frac{1}{4}\right)$
已知函数 $f(x)=\log _2(x+1)-x$ ，则不等式 $f(x)>0$ 的解集是（ ）
$\text{A.}$ $(1,+\infty)$
$\text{B.}$ $(0,+\infty)$
$\text{C.}$ $(0,1)$
$\text{D.}$ $(-1,0) \cup(1,+\infty)$
已知函数 $f ( x )=\log _2 x -( x -1)^2$ ，则不等式 $f(x) < 0$ 的解集为 $(\quad)$
$\text{A.}$ $(-\infty, 1) \cup(2,+\infty)$
$\text{B.}$ $(0,1) \cup(2,+\infty)$
$\text{C.}$ $(1,2)$
$\text{D.}$ $(1,+\infty)$
已知函数 $f ( x )=\log _2 x -\frac{3}{ x +1}$ ，则不等式 $f(x)>0$ 的解集是 $(\quad)$
$\text{A.}$ $(-1,2)$
$\text{B.}$ $(0,2)$
$\text{C.}$ $(2,+\infty)$
$\text{D.}$ $(-\infty,-1) \cup(-1,2)$
已知二次函数 $f(x)$ ，对任意的 $x \in R$ ，有 $f(2 x) < 2 f(x)$ ，则 $f(x)$ 的图象可能是
$\text{A.}$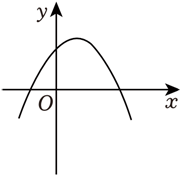 
$\text{B.}$ 
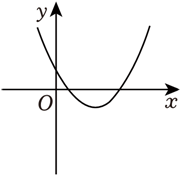$\text{C.}$ 
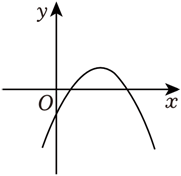$\text{D.}$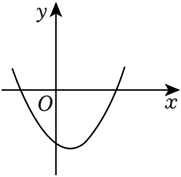 
不等式 $(x-1)(x-4) \geqslant 0$ 的解集是（ ）
$\text{A.}$ $\{x \mid x>4$ 或 $x < 1\}$
$\text{B.}$ $\{x \mid 1 < x < 4\}$
$\text{C.}$ $\{x \mid 1 \leqslant x \leqslant 4\}$
$\text{D.}$ $\{x \mid x \geqslant 4$ 或 $x \leqslant 1\}$
已知集合 $A=\{x \mid 2 < x < 4\}, B=\{x \mid(x-6)(x-3) \geqslant 0\}$ ，则（ ）
$\text{A.}$ $2 \in A \cap B$
$\text{B.}$ $3 \in A \cap B$
$\text{C.}$ $4 \in A \cup B$
$\text{D.}$ $5 \in A \cup B$
设 $x_1, x_2$ 是关于 $x$ 的方程 $x^2+(a-1) x+a+2=0$ 的根．若 $-1 < x_1 < $ $1,1 < x_2 < 2$ ，则实数 $a$ 的取值范围是（）
$\text{A.}$ $\left(-\frac{4}{3},-1\right)$
$\text{B.}$ $\left(-\frac{3}{4}, \frac{1}{2}\right)$
$\text{C.}$ $(-2,1)$
$\text{D.}$ $(-2,-1)$
解答题 （共 2 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $m+2 n=2$ ，且 $m>-1, n>0$ ．
（1）求 $\frac{1}{m+1}+\frac{2}{n}$ 的最小值；
（2）求 $\frac{m^2}{2 n+2}+\frac{4 n^2}{m+1}$ 的最小值．
已知 $a, b, c$ 为正实数且 $a+2 b+3 c=5$ ．
（1）求 $a^2+b^2+c^2$ 的最小值；
（2）当 $\sqrt{2 a b}+\sqrt{3 a c}+\sqrt{6 b c} \geqslant 5$ 时，求 $a+b+c$ 的值．