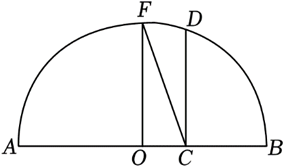
《几何原本》第二卷中的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多代数的定理都能够通过图形实现证明,并称之为无字证明.现有如图所示的图形,点 $F$ 在半圆 $O$ 上,且 $O F \perp A B$ ,点 $C$ 在直径 $A B$ 上运动.作 $C D \perp A B$ 交半圆 $O$ 于点 $D$ .设 $A C=a$ , $B C=b$ ,则由 $F C \geqslant C D$ 可以直接证明的不等式为
A
$\frac{a+b}{2} \geqslant \sqrt{a b}(a>0, b>0)$
B
$a^2+b^2 \geqslant 2 a b(a>0, \quad b>0)$
C
$\frac{2 a b}{a+b} \leqslant \sqrt{\frac{a^2+b^2}{2}}(a>0, b>0)$
D
$\sqrt{a b} \leqslant \sqrt{\frac{a^2+b^2}{2}}(a>0, b>0)$
E
F