单选题 （共 8 题 ），每题只有一个选项正确
某公司抽检盒装牛奶的容量, 超过标准容量的部分记为正数, 不足的部分记为负数. 从容量的角度看,以下四盒牛奶容量最接近标准的是
$\text{A.}$ $+0.8 \mathrm{~mL}$
$\text{B.}$ $-1.2 \mathrm{~mL}$
$\text{C.}$ $-0.5 \mathrm{~mL}$
$\text{D.}$ $+1 \mathrm{~mL}$
科学家发现了一种新型病毒, 其直径约为 $0.00000042 \mathrm{~m}, 0.00000042$ 这个数用科学记数法表 示为
$\text{A.}$ $0.42 \times 10^{-6}$
$\text{B.}$ $4.2 \times 10^{-6}$
$\text{C.}$ $4.2 \times 10^{-7}$
$\text{D.}$ $42 \times 10^{-8}$
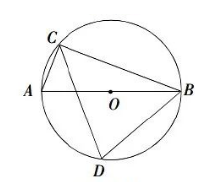
如图, $C 、 D$ 是 $\odot O$ 上直径 $A B$ 两侧的两点, 若 $\angle A B C=20^{\circ}$, 则 $\angle B D C$ 的度数是
$\text{A.}$ $50^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $80^{\circ}$
$\text{D.}$ $70^{\circ}$
若二次函数 $y=-x^2+b x+c$ 图象的顶点坐标为 $(-2,1)$, 则 $c$ 的值为
$\text{A.}$ $1$
$\text{B.}$ $-1$
$\text{C.}$ $-2$
$\text{D.}$ $-3$
某书店拿取高处书籍的登高梯如图位置摆放, 登高梯 $A C$ 的顶端 $A$ 恰好放在书架的第七层的 顶端. 已知登高梯的长度 $A C$ 为 3 米, 登高梯与地面的夹角 $\angle A C B$ 为 $72^{\circ}$, 则书架第七层顶端 离地面的高度 $A B$ 为
$\text{A.}$ $3 \sin 72^{\circ}$ 米
$\text{B.}$ $\frac{3}{\sin 72^{\circ}}$ 米
$\text{C.}$ $3 \cos 72^{\circ}$ 米
$\text{D.}$ $\frac{3}{\cos 72^{\circ}}$ 米
在 $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B \neq A C$. 用无刻度的直尺和圆规在 $B C$ 边上找一点 $D$, 使 $\triangle A C D$ 为等腰三角形.下列作法不正确的是
$\text{A.}$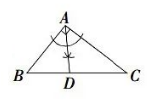 
$\text{B.}$ 
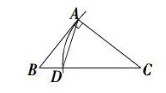$\text{C.}$ 
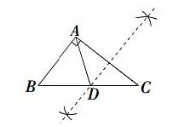$\text{D.}$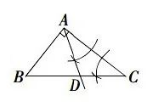 
如图, 在平面直角坐标系中, 矩形 $A B C D$ 的顶点 $A, B$ 分别落在 $y$ 轴、 $x$ 轴的正半轴上, $A(0,2), B C=2 A B$. 若反比例函数 $y=\frac{k}{x}(k>0)$ 经过 $C, D$ 两点,则 $k$ 的值为
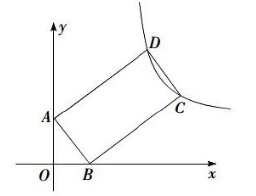
$\text{A.}$ 12
$\text{B.}$ 18
$\text{C.}$ 24
$\text{D.}$ 36
填空题 （共 6 题 ），请把答案直接填写在答题纸上
若关于 $x$ 的一元二次方程 $2 x^2-3 x-m=0$ 有两个相等的实数根, 则 $m=$
将一副三角板和一个直尺按如图所示的位置摆放, 则 $\angle 1$ 的度数为 （ ） 度.
如图, 在平面直角坐标系中, 等边三角形 $O A B$ 的边 $O B$ 在 $x$ 轴上, 点 $A$ 在第一象限, $O B=3$, 点 $C$ 在线段 $O A$ 上, 且 $O C=2$. 将 $\triangle O A B$ 沿射线 $O A$ 的方向平移至 $\triangle C A_1 B_1$ 的位置, 此时 点 $A_1$ 的坐标是
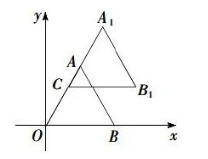
如图①, 一个扇形纸片的圆心角为 $90^{\circ}$, 半径为 4 . 如图 ②, 将这张扇形纸片折叠, 使点 $A$ 与点 $O$ 恰好重合, 折痕为 $C D$, 图中阴影为重合部分, 则阴影部分的面积 为
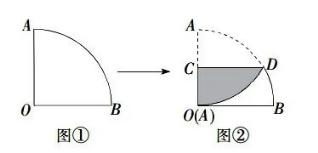
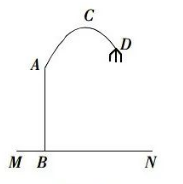
如图, 一款落地灯的灯柱 $A B$ 垂直于水平地面 $M N$, 高度为 $1.6$ 米, 支架部分的形状为开口向下的抛物线, 其顶点 $C$ 距灯柱 $A B$ 的水平距离为 $0.8$ 米, 距地面的高度为 $2.4$ 米,灯罩顶端 $D$ 距灯柱 $A B$ 的水平距离为 $1.4$ 米, 则灯罩顶端 $D$ 距地面的高度为 （ ） 米.
解答题 （共 10 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求值: $(x+1)(x-1)-x(x-3)$, 其中 $x=\sqrt{2}$.
某景区检票口有 A、B、C 共 3 个检票通道, 甲, 乙两人到该景区游玩, 两人分别从 3 个 检票通道中随机选择一个检票.
(1)甲选择 $\mathrm{A}$ 检票通道的概率是
(2)用列表法或树状图法求甲、乙两人选择的检票通道恰好相同的概率.
近期, 受俄乌局势影响, 国内汽油价格不断上涨. 请你根据下面的信息 (如图), 计算今 年 4 月份汽油的价格.
如图是由小正方形组成的 $8 \times 8$ 网格, 每个小正方形的顶点叫做格点, 仅用无刻度的直 尺在给定的网格中完成画图, 并保留必要的作图痕迹.
(1) 在图 1 中, 在直线 $B C$ 的下方作格点 $D$ 使 $A D \perp B C$, 连结 $A D$, 垂足为 $H$.
(2) 在图 2 中找出所有可能的格点 $F$, 使 $\triangle B C F$ 是以 $B C$ 为直角边的等腰直角三角形, 并画出 $\triangle B C F$.
(3) 在图 3 中的线段 $B C$ 上画出点 $G$, 使 $\angle A G C=45^{\circ}$.
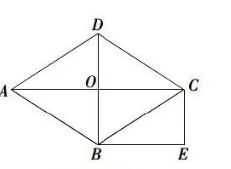
如图, 菱形 $A B C D$ 中, $A C 、 B D$ 相交于点 $O$, 过点 $B$ 作 $B E \perp B D$, 且 $B E=O C$, 连结 $C E$.
(1) 求证: 四边形 $O C E B$ 是矩形.
(2) 连接 $D E$, 若 $\sin \angle C A B=\frac{3}{5}$, 则 $\tan \angle B D E$ 的值是
党的二十大于 2022 年 11 月 8 日至 11 日在北京举行, 为了调查大学生对大会精神的了 解情况, 甲、乙两校进行了相关知识测试, 在两校各随机抽取 20 名大学生的测试成绩 (百分 制), 并对数据(成绩) 进行了整理、描述和分析. 下面给出了部分信息.
a. 甲校 20 名大学生成绩的频数分布表和频数分布直方图如图:
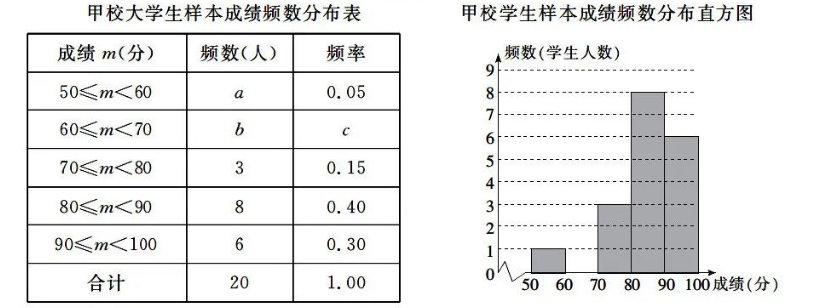
b. 甲校成绩在 $80 \leqslant m < 90$ 的这一组的具体成绩是: $86 ; 86 ; 87 ; 87 ; 88 ; 89 ; 89 ; 89$
c. 甲、乙两校成绩的统计数据如表所示:
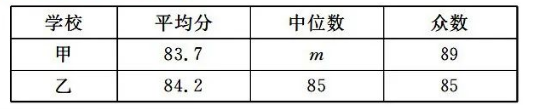
根据以如图表提供的信息, 解答下列问题:
(1) 表中 $a=$, $M=$
(2)补全甲校大学生样本成绩频数分布直方图.
(3)在此次测试中, 某学生的成绩是 86 分, 在他所属学校排在前 10 名, 由表中数据可知该学 生是 校的学生(填“甲”或“乙”).
(4)若甲校共有 1600 人, 成绩不低于 80 分为“优秀”, 则甲校成绩“优秀”的人数约为多少人?
为了学生的身体健康, 学校课桌、凳的高度都是按照一定的关系科学设计的. 研究表明: 课桌的高度与椅子的高度符合一次函数关系. 小明测量了一套课桌、椅对应的四档高度, 得到数据如下表:
(1) 在上面的表格中, 有一个数据被污染了, 则被污染的数据为
(2) 设课桌的高度为 $y(\mathrm{~cm})$, 椅子的高度为 $x(\mathrm{~cm}$ ), 求 $y$ 与 $x$ 的函数关系式 (不必写出自变量 的取值范围).
(3) 小明放学回到家, 又测量了家里的写字台的高度为 $77 \mathrm{~cm}$, 登子的高度为 $41 \mathrm{~cm}$, 请你判断 小明家里的写字台与凳子是否符合科学设计, 并说明理由.
旋转是一种重要的图形变换, 当图形中有一组邻边相等时往往可以通过旋转解决问题.
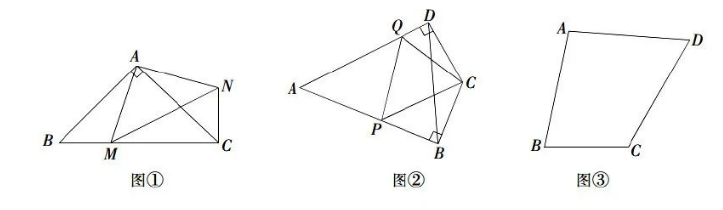
(1) 尝试解决: 如图①, 在等腰 Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $M$ 是 $B C$ 上的一点, $B M=2 \mathrm{~cm}, C M=4 \mathrm{~cm}$, 将 $\triangle A B M$ 绕点 $A$ 旋转后得到 $\triangle A C N$, 连接 $M N$, 求 $A M$ 的长度.
(2) 类比探究: 如图②, 在“筝形”四边形 $A B C D$ 中, $A B=A D=m, C B=C D, A B \perp B C$ 于点 $B$, $A D \perp C D$ 于点 $D$, 点 $P 、 Q$ 分别是 $A B 、 A D$ 上的点, 且 $\angle P C B+\angle Q C D=\angle P C Q$, 则 $\triangle A P Q$ 的周长为 . (结果用含 $m$ 的代数式表示)
(3) 拓展应用: 如图③, 已知四边形 $A B C D, A D=C D, \angle A D C=60^{\circ}, \angle A B C=75^{\circ}, A B=4 \sqrt{2}$, $B C=4$, 直接写出四边形 $A B C D$ 的面积.
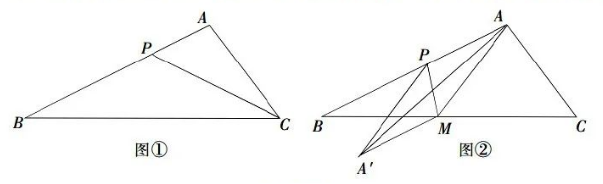
如图①, 在 $\triangle A B C$ 中, $B C=11, A C=5, \tan \angle A C B=\frac{4}{3}$, 点 $P$ 从点 $A$ 出发, 沿折线 $A B-B C$ 向点 $C$ 运动, 点 $P$ 在 $A B$ 边上以每秒 $\sqrt{5}$ 个单位长度的速度运动, 在 $B C$ 边上以每秒 2 个单位 长度的速度运动, 点 $P$ 的运动时间为 $t$ 秒.
(1) $A B$ 的长为
(2) 用含有 $t$ 的代数式表示线段 $P B$ 的长.
(3) 在点 $P$ 运动的过程中, 连结 $C P$, 当 $\angle A P C=2 \angle B$ 时, 求 $B P$ 的长.
(4) 如图②, 点 $M$ 为 $B C$ 边上一点, $B M=5$, 连结 $A M 、 M P$, 将 $\triangle A M P$ 绕线段 $M P$ 中点旋转 $180^{\circ}$ 得到 $\triangle A^{\prime} M P$, 连结 $A A^{\prime}$, 当 $A A^{\prime}$ 将 $\triangle A B C$ 的面积分成 $4: 7$ 两部分时, 直接写出 $t$ 的值.
在平面直角坐标系中, 抛物线 $y=x^2+b x+c$ 经过点 $A(0,3)$ 和点 $B(1,0)$, 顶点为 $D$, 点 $P$ 是抛物线上一动点, 其横坐标为 $m$.
(1) 求该抛物线函数关系式.
(2) 当点 $P$ 在抛物线对称轴左侧时, 过点 $P$ 作 $P C \perp y$ 轴交抛物线对称轴于点 $C$, 若 $\tan \angle P D C=\frac{1}{3}$, 求 $m$ 的值.
(3) 记抛物线在点 $P 、 B$ 两点之间的部分为图象 $G$ (包含 $P 、 B$ 两点), 设图象 $G$ 的最高点与最 低点的纵坐标之差为 $d$, 当 $1 \leqslant d \leqslant 4$ 时, 求 $m$ 的取值范围.
(4) 点 $Q(2 m-1,4-2 m)$ 是平面内一点, 当 $P Q$ 不与坐标轴平行时, 以 $P Q$ 为对角线构造矩形 $P M Q N$, 使矩形各边与坐标轴垂直, 当抛物线在矩形 $P M Q N$ 内的部分所对应的函数值 $y$ 随 $x$ 的增大而增大或 $y$ 随 $x$ 的增大而减小时, 直接写出 $m$ 的取值范围.