党的二十大于 2022 年 11 月 8 日至 11 日在北京举行, 为了调查大学生对大会精神的了 解情况, 甲、乙两校进行了相关知识测试, 在两校各随机抽取 20 名大学生的测试成绩 (百分 制), 并对数据(成绩) 进行了整理、描述和分析. 下面给出了部分信息.
a. 甲校 20 名大学生成绩的频数分布表和频数分布直方图如图:


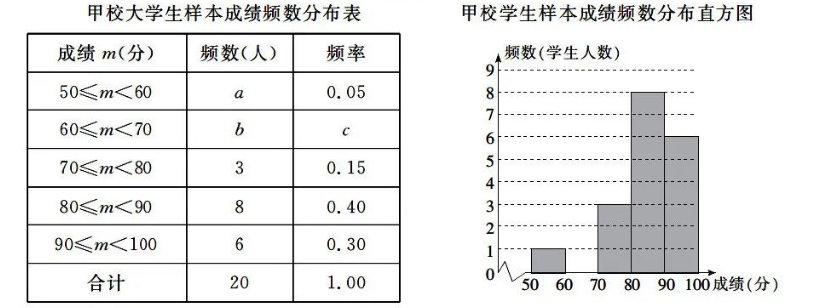
b. 甲校成绩在 $80 \leqslant m < 90$ 的这一组的具体成绩是: $86 ; 86 ; 87 ; 87 ; 88 ; 89 ; 89 ; 89$
c. 甲、乙两校成绩的统计数据如表所示:


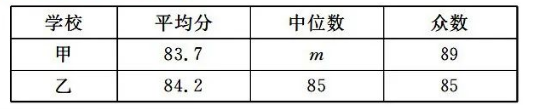
根据以如图表提供的信息, 解答下列问题:
(1) 表中 $a=$, $M=$
(2)补全甲校大学生样本成绩频数分布直方图.
(3)在此次测试中, 某学生的成绩是 86 分, 在他所属学校排在前 10 名, 由表中数据可知该学 生是 校的学生(填“甲”或“乙”).
(4)若甲校共有 1600 人, 成绩不低于 80 分为“优秀”, 则甲校成绩“优秀”的人数约为多少人?