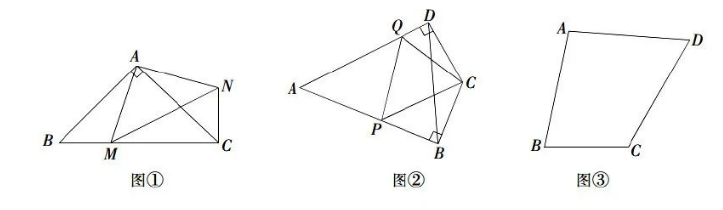
旋转是一种重要的图形变换, 当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1) 尝试解决: 如图①, 在等腰 Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $M$ 是 $B C$ 上的一点, $B M=2 \mathrm{~cm}, C M=4 \mathrm{~cm}$, 将 $\triangle A B M$ 绕点 $A$ 旋转后得到 $\triangle A C N$, 连接 $M N$, 求 $A M$ 的长度.
(2) 类比探究: 如图②, 在“筝形”四边形 $A B C D$ 中, $A B=A D=m, C B=C D, A B \perp B C$ 于点 $B$, $A D \perp C D$ 于点 $D$, 点 $P 、 Q$ 分别是 $A B 、 A D$ 上的点, 且 $\angle P C B+\angle Q C D=\angle P C Q$, 则 $\triangle A P Q$ 的周长为 . (结果用含 $m$ 的代数式表示)
(3) 拓展应用: 如图③, 已知四边形 $A B C D, A D=C D, \angle A D C=60^{\circ}, \angle A B C=75^{\circ}, A B=4 \sqrt{2}$, $B C=4$, 直接写出四边形 $A B C D$ 的面积.