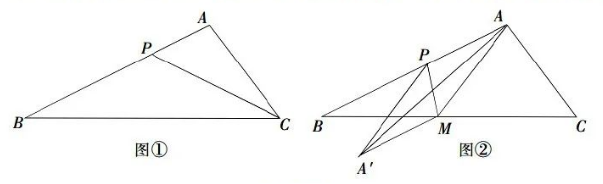
如图①, 在 $\triangle A B C$ 中, $B C=11, A C=5, \tan \angle A C B=\frac{4}{3}$, 点 $P$ 从点 $A$ 出发, 沿折线 $A B-B C$ 向点 $C$ 运动, 点 $P$ 在 $A B$ 边上以每秒 $\sqrt{5}$ 个单位长度的速度运动, 在 $B C$ 边上以每秒 2 个单位 长度的速度运动, 点 $P$ 的运动时间为 $t$ 秒.
(1) $A B$ 的长为
(2) 用含有 $t$ 的代数式表示线段 $P B$ 的长.
(3) 在点 $P$ 运动的过程中, 连结 $C P$, 当 $\angle A P C=2 \angle B$ 时, 求 $B P$ 的长.
(4) 如图②, 点 $M$ 为 $B C$ 边上一点, $B M=5$, 连结 $A M 、 M P$, 将 $\triangle A M P$ 绕线段 $M P$ 中点旋转 $180^{\circ}$ 得到 $\triangle A^{\prime} M P$, 连结 $A A^{\prime}$, 当 $A A^{\prime}$ 将 $\triangle A B C$ 的面积分成 $4: 7$ 两部分时, 直接写出 $t$ 的值.