单选题 （共 19 题 ），每题只有一个选项正确
2023 年我国首套高温超导电动悬浮全要素试验系统完成首次悬浮运行, 实线重要技术突破。设该系统的试验列车质量为 $m$, 某次 试 验 中 列车以速率 $v$ 在 平 直 轨道 上匀速行驶, 刹车时牵引系统处于关闭状态, 制动装置提供大小为 $F$ 的制动力, 列车减速直至停止。若列车行驶时始终受到大小为 $f$ 的空气阻力, 则
$\text{A.}$ 列车减速过程的加速度大小 $a=\frac{F}{m}$
$\text{B.}$ 列车减速过程 $F$ 的冲量为 $m v$
$\text{C.}$ 列车减速过程通过的位移大小为 $\frac{m v^2}{2(F+f)}$
$\text{D.}$ 列车匀速行驶时, 牵引系统的输出功率为 $(f+F) v$
两节动车的额定功率分别为 $P_1$ 和 $P_2$, 在某平直铁轨上能达到的最大速度分别为 $v_1$ 和 $v_2$ 。现将它们编成动车组, 设每节动车运行时受到的阻力在编组前后不变, 则该动车组在此铁轨上能达到的最大速度为
$\text{A.}$ $\frac{P_1 v_1+P_2 v_2}{P_1+P_2}$
$\text{B.}$ $\frac{P_1 v_2+P_2 v_1}{P_1+P_2}$
$\text{C.}$ $\frac{\left(P_1+P_2\right) v_1 v_2}{P_1 v_1+P_2 v_2}$
$\text{D.}$ $\frac{\left(P_1+P_2\right) v_1 v_2}{P_1 v_2+P_2 v_1}$
质量为 $M$ 的玩具动力小车在水平面上运动时, 牵引力 $F$ 和受到的阻力 $f$ 均为恒力, 如图所示, 小车用一根不可伸长的轻绳拉着质量为 $m$ 的物体由静止开始运动。当小车拖动物体行驶的位移为 $S_1$ 时, 小车达到额定功率, 轻绳从物体上脱落。物体继续滑行一段时间后停下, 其总位移为 $S_2$ 。物体与地面间的动摩擦因数不变, 不计空气阻力。小车的额定功率 $P_0$ 为
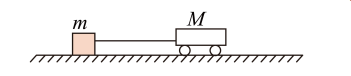
$\text{A.}$ $\sqrt{\frac{2 F^2(F-f)\left(S_2-S_1\right) S_1}{(M+m) S_2-M S_1}}$
$\text{B.}$ $\sqrt{\frac{2 F^2(F-f)\left(S_2-S_1\right) S_1}{(M+m) S_2-m S_1}}$
$\text{C.}$ $\sqrt{\frac{2 F^2(F-f)\left(S_2-S_1\right) S_2}{(M+m) S_2-M S_1}}$
$\text{D.}$ $\sqrt{\frac{2 F^2(F-f)\left(S_2-S_1\right) S_2}{(M+m) S_2+m S_1}}$
小明用额定功率为 $1200 \mathrm{~W}$ 、最大拉力为 $300 \mathrm{~N}$ 的提升装置, 把静置于地面的质量为 $20 \mathrm{~kg}$ 的重物坚直提升到高为 $85.2 \mathrm{~m}$ 的平台, 先加速再匀速, 最后做加速度大小不超过 $5 \mathrm{~m} / \mathrm{s}^2$ 的匀减速运动, 到达平台的速度刚好为零, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 则提升重物的最短时间为
$\text{A.}$ $13.2 \mathrm{~s}$
$\text{B.}$ $14.2 s$
$\text{C.}$ $15.5 \mathrm{~s}$
$\text{D.}$ $17.0 \mathrm{~s}$
近年来一批国产电车正在强势崛起。现有某电车自重 2 吨, 额定功率 $360 \mathrm{~kW}$ 。在某次电车性能测试中, 电车以额定功率启动, 从 0 加速到 $108 \mathrm{~km} / \mathrm{h}$ 用时 $5 s$, 再经过 $20 \mathrm{~s}$ 后达到最大速度 $216 \mathrm{~km} / \mathrm{h}$ 。假设电车运动过程中所受阻力不变,则下列说法中正确的是
$\text{A.}$ 电车前 $5 s$ 加速过程中加速度不变
$\text{B.}$ 小车所受阻力为 $12000 \mathrm{~N}$
$\text{C.}$ 从静止加速到最大速度, 电车行驶的位移为 900 米
$\text{D.}$ 当电车速度为 $40 \mathrm{~m} / \mathrm{s}$ 时, 其加速度是 $2 \mathrm{~m} / \mathrm{s}^2$
目前,我国在人工智能和无人驾驶技术方面已取得较大突破。为测验某项无人驾驶技术, 某公司对一款无人驾驶汽车的性能进行了测试: 让质量为 $m$ 的汽车沿一山坡直线行驶, 测试中发现, 下坡时若关掉油门, 则汽车的速度大小保持不变; 若以恒定的功率 $P$ 上坡, 则汽车从静止启动做加速运动, 发生位移 $s$ 时速度刚好达到最大值 $v_m$ 。设汽车在上坡和下坡过程中所受阻力的大小保持不变, 下列说法不正确的是
$\text{A.}$ 关掉油门后的下坡过程,汽车的机械能是守恒的
$\text{B.}$ 关掉油门后的下坡过程,坡面对汽车的冲量不为零
$\text{C.}$ 上坡过程中, 当汽车速度达到 $\frac{v_m}{2}$ 时, 加速度 $a=\frac{P}{m v_m}$
$\text{D.}$ 上坡过程中,汽车的速度由 0 增至 $v_m$ 所用的时间 $\frac{m v_m^2}{2 P}+\frac{s}{v_m}$
如图所示, 高铁动车使从天津到北京的通行时间缩短在半小时左右, 便利出行。假设此高铁动车启动后沿平直轨道行驶, 发动机的功率恒为 $P$ 且行驶过程中受到的阻力大小恒定。已知动车的质量为 $m$, 最高行驶速度 $v_m=350 \mathrm{~km} / \mathrm{h}$ 。则下列说法正确的是
$\text{A.}$ 当动车的速度为 $\frac{v_m}{4}$ 时, 动车的加速度大小为 $\frac{3 P}{m v_m}$
$\text{B.}$ 由题目信息无法估算天津到北京铁路的长度
$\text{C.}$ 从启动到速度为 $v_m$ 的过程中, 动车牵引力所做的功为 $\frac{1}{2} m v_m^2$
$\text{D.}$ 行驶过程中动车受到的阻力大小为 $P v_m$
共享电动车已经成为我们日常生活中不可或缺的重要交通工具, 如图所示, 某共享电动车和驾驶员的总质量为 $100 \mathrm{~kg}$, 电动车的额定功率为 $500 \mathrm{~W}$ 。若电动车从静止开始以额定功率在水平路面沿直线行驶, 行驶中最大速度为 $5 \mathrm{~m} / \mathrm{s}$, 假定行驶中所受阻力恒定, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$ 。下列说法正确的是
$\text{A.}$ 电动车受到的阻力大小为 $100 \mathrm{~N}$
$\text{B.}$ 加速阶段, 电动车的加速度保持不变
$\text{C.}$ 当电动车的速度为 $2.5 \mathrm{~m} / \mathrm{s}$ 时, 其加速度大小为 $2 \mathrm{~m} / \mathrm{s}^2
$\text{D.}$ 若电动车从静止开始以 $2 \mathrm{~m} / \mathrm{s}^2$ 的加速度匀加速启动, 匀加速时间共 $5 \mathrm{~s}$
2023 年 11 月 10 日, 我国首条超高速低真空管道磁浮交通系统 - - 高速飞车大同 (阳高) 试验线工程完工, 其特点是全封闭真空管道和磁悬浮运输。如图所示, 高速飞车的质量为 $m$, 额定功率为 $P$, 高速飞车在平直轨道上从静止开始运动, 先以加速度 $a$ 做匀加速直线运动, 加速过程中达到额定功率 $P$ 。后又经过一段时间达到该功率下的最大速度, 若高速飞车行驶过程中所受到的阻力为 $F_f$ 且保持不变, 则下列说法正确的是
$\text{A.}$ 高速飞车匀加速直线运动过程中达到的最大速度为 $\frac{P_0}{m a}$
$\text{B.}$ 高速飞车匀加速直线运动的时间为 $\frac{P_0}{a\left(F_f-m a\right)}$
$\text{C.}$ 高速飞车匀加速直线运动的位移为 $\frac{P_0^2}{2 a\left(F_f+m a\right)^2}$
$\text{D.}$ 高速飞车在整个加速过程中牵引力做功等于 $\frac{m P_0^2}{2 F_f^2}$
高铁已成为中国的 “国家名片”, 是大多数人出行的首选。提高列车运动速率的有效途径是增大发动机的功率和减小阻力。某列车由若干节额定功率均为 $P$ 的动力车厢组成, 行驶时所受的阻力与速率的二次方成正比, 即 $f=k v^2$, 只启用一节动力车厢时列车能达到的最大速度为 $v_m$ 。列车由静止开始运动, 下列说法正确的是
$\text{A.}$ 若列车匀加速启动, 则牵引力恒定
$\text{B.}$ 若列车输出功率恒定, 则做匀加速运动
$\text{C.}$ 若启用 4 节动力车厢, 则列车的最大速度为 $4 v_m$
$\text{D.}$ 若列车最大速度提高到 $2 v_m$, 则需要启用 8 节动力车厢
我国新能源电动汽车越来越受到大众的喜爱。一款电动家用轿车在某次测试中先匀加速启动达到额定功率后以额定功率继续加速运动。测得轿车由静止加速到 $30 \mathrm{~m} / \mathrm{s}$ 时间仅为 $3 \mathrm{~s}$, 则轿车在该段时间内
$\text{A.}$ 牵引力不断增大
$\text{B.}$ 位移大于 $45 m$
$\text{C.}$ 平均速度为 $15 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 匀加速阶段的加速度为 $10 \mathrm{~m} / \mathrm{s}^2$
某探究小组对一辆新能源小车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动, 并将小车运动的全过程记录下来, 通过处理转化为 $v-t$ 图像, 如图所示 (除 2 - $10 s$ 时间段图线为曲线外, 其余时间段图线均为直线)。已知小车运动的过程中, 2 $14 \mathrm{~s}$ 时间段内小车的功率保持不变, 在第 $14 \mathrm{~s}$末撤去动力而让小车自由滑行, 小车的质量为 $1.0 \mathrm{~kg}$, 可认为在整个运动过程中小车所受到的阻力大小不变。以下对小车的描述正确的是
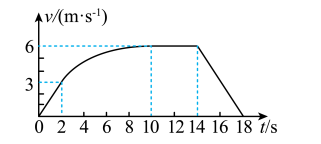
$\text{A.}$ 小车所受的阻力大小为 $3 N$
$\text{B.}$ 小车匀速行驶阶段的功率为 $9 \mathrm{~W}$
$\text{C.}$ 小车在加速运动过程中位移的大小为 $40 \mathrm{~m}$
$\text{D.}$ 小车在前 $2 s$ 受到的合力大小大于阻力大小
一辆摩托车在平直的公路上由静止启动, 摩托车所受牵引力 $F$ 随时间 $t$ 变化关系如图所示。摩托车总质量为 $200 \mathrm{~kg}$, 额定功率为 $2 \times 10^4 W$, 运动过程所受阻力恒定, 则
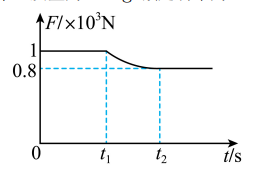
$\text{A.}$ 摩托车在 $0 \sim t_1$ 时间内做匀加速运动, $t_1 \sim t_2$ 时间内做减速运动
$\text{B.}$ 摩托车在 $0 \sim t_1$ 时间内的加速度为 $5 \mathrm{~m} / \mathrm{s}^2$
$\text{C.}$ 运动过程中摩托车的最大速度为 $20 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 摩托车匀加速行驶的时间为 $20 \mathrm{~s}$
某学校科技小组制作的太阳能驱动小车如图甲所示。太阳能驱动小车的质量 $M=40 \mathrm{~kg}$, 小车在水平地面上由静止开始做直线运动, 一段时间内小车的速度 $v$ 与牵引力的功率 $P$ 随时间变化的图像分别如图乙、丙所示。已知 $3 \mathrm{~s}$ 末小车牵引力的功率达到额定功率, $10 \mathrm{~s}$ 末小车的速度达到最大值, $14 \mathrm{~s}$ 末关闭电动机, 再经过一段时间小车停止运动。设整个过程中太阳能驱动小车受到的阻力恒定。下列说法正确的是
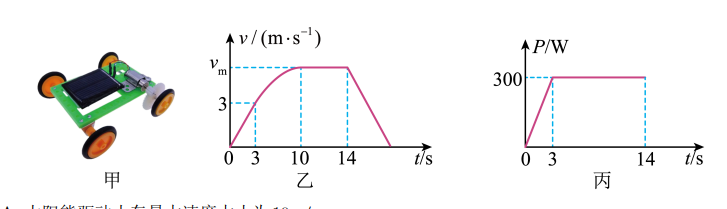
$\text{A.}$ 太阳能驱动小车最大速度大小为 $10 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ 太阳能驱动小车受到的阻力大小为 $100 N$
$\text{C.}$ 整个过程中, 太阳能驱动小车克服阻力做功为 $3750 \mathrm{~J}$
$\text{D.}$ 关闭电动机后, 太阳能驱动小车经过 $5 s$ 停止运动
质量为 $400 \mathrm{~kg}$ 的赛车在平直赛道上以恒定功率加速, 受到的阻力不变, 其加速度 $a$ 与速度的倒数 $\frac{1}{v}$ 的关系如图所示, 则赛车
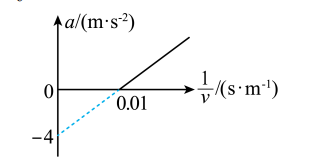
$\text{A.}$ 速度随时间均匀增大
$\text{B.}$ 加速度随时间均匀增大
$\text{C.}$ 输出功率为 $16 \mathrm{~kW}$
$\text{D.}$ 所受阻力大小为 $1600 \mathrm{~N}$
一辆汽车在水平平直公路上由静止开始匀加速启动, 汽车的输出功率与速度的关系如图所示, 当汽车的速度达到 $v_0$ 后功率保持不变, 汽车能达到的最大速度为 $2 v_0$ 。已知汽车的质量为 $m$, 运动过程中所受的阻力恒为 $f$,下列说法正确的是
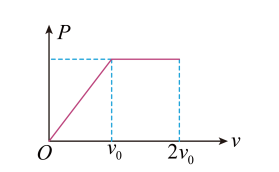
$\text{A.}$ 汽车的最大功率为 $2 f v_0$
$\text{B.}$ 汽车匀加速时的加速度大小为 $\frac{f}{2 m}$
$\text{C.}$ 汽车做匀加速直线运动的时间为 $\frac{m v_0}{2 f}$
$\text{D.}$ 汽车的速度从 $v_0$ 增加到 $2 v_0$ 的过程中, 其加速度保持不变
图甲是全球最大回转自升塔式起重机, 它的开发标志着中国工程用超大吨位塔机打破长期依赖进口的局面, 也意味着中国桥梁及铁路施工装备进一步迈向世界前列。该起重机某次从 $t=0$ 时刻由静止开始提升质量为 $m$ 的物体, 其 $a-t$ 图像如图乙所示, $t_1 \sim t_2$ 时间内起重机的功率为额定功率, 不计其他阻力,重力加速度为 $g$, 则以下说法正确的是
$\text{A.}$ 该起重机的额定功率为 $m a_0^2 t_1$
$\text{B.}$ 该起重机的额定功率为 $\left(\mathrm{mg}+m a_0\right) a_0\left(t_2-t_1\right)$
$\text{C.}$ $0 \sim t_1$ 和 $t_1 \sim t_2$ 时间内牵引力做的功之比为 $t_1: 2\left(t_2-t_1\right)$
$\text{D.}$ $0 \sim t_1$ 和 $t_1 \sim t_2$ 时间内牵引力做的功之比为 $t_1: 2 t_2$
一起重机用钢绳提起静止在地面上的重物, 开始在坚直方向上做匀加速运动, 然后做匀速运动。重物上升高度为 $h$, 运动时间为 $t$, 加速度为 $a$, 动能为 $E_k$, 起重机功率为 $P$, 下列图像能描述上述过程的是
$\text{A.}$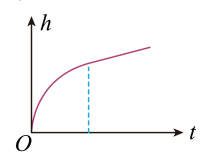 
$\text{B.}$ 
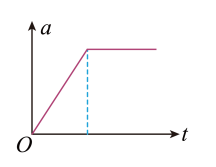$\text{C.}$ 
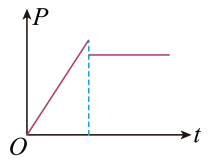$\text{D.}$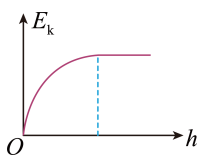 
一起重装置把静置于地面上的重物坚直向上提升的过程中, 功率随时间变化的 $P-t$ 图像如图所示。在 $t=1 \mathrm{~s}$ 时, 重物上升的速度达到最大速度的一半, 在 $t=3 \mathrm{~s}$ 时, 达到最大速度 $v_m=20 \mathrm{~m} / \mathrm{s}$ 。在 $t=6 \mathrm{~s}$时, 重物再次匀速上升, 取 $g=10 \mathrm{~m} / \mathrm{s}^2$, 不计一切阻力。下列说法正确的是
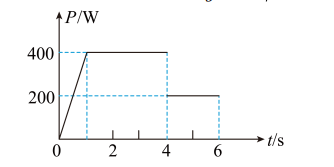
$\text{A.}$ 重物的质量为 $4 \mathrm{~kg}$
$\text{B.}$ 在 $t=1 \mathrm{~s}$ 时, 重物加速度大小 $a=20 \mathrm{~m} / \mathrm{s}^2$
$\text{C.}$ $0 \sim 6 s$ 时间内,重物上升的高度 $h=85 \mathrm{~m}$
$\text{D.}$ 在 4 $6 s$ 时间内, 重物做加速度逐渐增大的减速运动
多选题 （共 1 题 ），每题有多个选项正确
如图甲所示, 某同学用轻绳通过定滑轮提升一重物。运用传感器 (未在图中画出) 测得此过程中不同时刻被提升重物的速度 $v$ 与对轻绳的拉力 $F$, 并描绘出 $v-\frac{1}{F}$ 图像。假设某次实验得到的图像如图乙所示, 线段 $B C$ 与 $v$ 轴平行, 线段 $A B$ 的延长线过原点。实验中还测得重物由静止开始经过 $t=1.4 \mathrm{~s}$, 速度增加到 $v_A=3.0 \mathrm{~m} / \mathrm{s}$, 此后物体做匀速运动。取重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$, 滑轮质量、摩擦和其他阻力均可忽略不计。
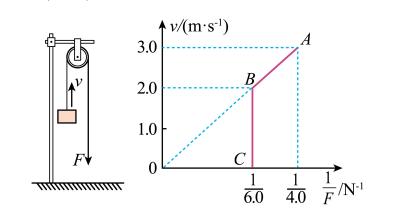
$\text{A.}$ $B$ 点时拉力的功率为 $12 W$
$\text{B.}$ 重物的质量为 $4 \mathrm{~kg}$
$\text{C.}$ 重物在 $A B$ 段做变加速运动, 在 $B C$ 段做匀加速运动
$\text{D.}$ 重物在 $A B$ 段的位移为 $3.15 \mathrm{~m}$