单选题 (共 12 题 ),每题只有一个选项正确
已知 $z=1-2 i$, 则 $z(\bar{z}-i)$ 的模长为
$\text{A.}$ 4
$\text{B.}$ $\sqrt{10}$
$\text{C.}$ 2
$\text{D.}$ 10
设集合 $M=\{x \in N \mid y=\lg (3-x)\}, N=\left\{y \mid y=2^x, x \in M\right\}$, 则
$\text{A.}$ $M \subseteq N$
$\text{B.}$ $N \subseteq M$
$\text{C.}$ $M \cap N=\{0,1,2\}$
$\text{D.}$ $M \cup N=\{0,1,2,4\}$
命题 “存在实数 $x_0$, 使 $e^{x_0}>\frac{1}{x_0}$ ” 的否定是
$\text{A.}$ 不存在实数 $x_0$, 使 $e^{x_0} \leq \frac{1}{x_0}$
$\text{B.}$ 存在实数 $x_0$, 使 $e^{x_0} \leq \frac{1}{x_0}$
$\text{C.}$ 对任意的实数 $x$, 都有 $e^x \leq \frac{1}{x}$
$\text{D.}$ 对任意的实数 $x$, 都有 $e^x>\frac{1}{x}$
黑洞原指非常奇怪的天体, 它体积小, 密度大, 吸引力强, 任何物体到了它那里都别 想再出来, 数字中也有类似的 “黑洞”, 任意取一个数字串, 长度不限, 依次写出该数 字串中偶数的个数、奇数的个数以及总的数字个数, 把这三个数从左到右写成一个新数 字串; 重复以上工作, 最后会得到一个反复出现的数字, 我们称它为 “数字黑洞”, 如 果把这个数字设为 $a$, 则 $\sin \left(\frac{a}{2} \pi+\frac{\pi}{6}\right)=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{2}$
$\text{D.}$ $-\frac{\sqrt{3}}{2}$
已知 $\left(\sqrt{x}+\frac{2}{x^2}\right)^n$ 的展开式中, 第 3 项的系数与倒数第 3 项的系数之比为 $\frac{1}{4}$, 则展开 式中二项式系数最大的项为第()项
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
已知 $F$ 为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的另焦点, $A$ 为 $C$ 的左顶点, $B$ 为 $C$ 上 的点, 且 $B F$ 垂直于 $ x$ 轴, 若直线 $A B$的倾角为$\frac{\pi}{4} $,则双曲线 $C$ 的离心率为
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ 2
$\text{D.}$ 3
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 满足 $a_1=1, a_2=3,2 \sqrt{S_n}=\sqrt{S_{n+1}}+\sqrt{S_{n-1}}(n \geq 2)$,
则 $a_{2022}=$
$\text{A.}$ 4043
$\text{B.}$ 4042
$\text{C.}$ 4041
$\text{D.}$ 4040
已知 $a=\sin \frac{\pi}{4}, b=e^{\ln \frac{1}{2}}, c=\frac{\pi}{6}$ 执行如图所示的程序框图, 输出的值为

$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\frac{\pi}{6}$
$\text{D.}$ $1$
双曲函数在实际生活中有着非常重要的应用, 比如悬链桥. 在数学中, 双曲函数是一 类与三角函数类似的函数, 最基础的是双曲正弦函数 $\sinh x=\frac{e^x-e^{-x}}{2}$ 和双曲余弦函数 $\cosh x=\frac{e^x+e^{-x}}{2}$. 下列结论错误的是
$\text{A.}$ 双曲正弦函数图象关于原点中心对称, 双曲余弦函数图象关于 $y$ 轴对称
$\text{B.}$ 若直线 $y=m$ 与双曲余弦函数图象 $C_1$ 和双曲正弦函数图象 $C_2$ 共有三个交点, 则 $m \geq 1$
$\text{C.}$ 双曲余弦函数图象 $C_1$ 总在双曲正弦函数图象 $C_2$ 上方
$\text{D.}$ 双曲正弦函数 $\sinh x=\frac{e^x-e^{-x}}{2}$ 导函数的图象与双曲余弦函数图象重合
已知四条直线 $l_1: y=0, l_2: y=x, l_3: y=3 x-2, l_4: y=3 x+2$, 从这四条直线 中任取两条, 这两条直线都与函数 $f(x)=x^3$ 的图象相切的概率为
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{6}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{1}{3}$
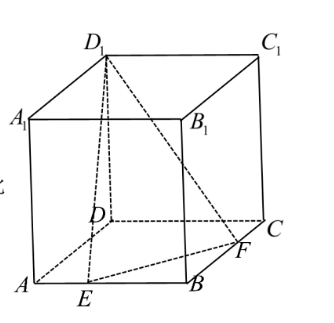
如图, 直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 的底面是边长为 3 的正方形, 侧棱长为 $4, E, F$ 分别在 $A B, B C$ 上, 且 $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A B} ,\overrightarrow{C F}=\frac{1}{3} \overrightarrow{C B}$, 过 $D_1, E, F$ 的平面记为 $a$, 则下 列说法中正确的个数是
① $D_1 F$ 与面 $A B C D$ 所成角的正切值为 $\frac{2 \sqrt{10}}{5}$;
②平面 $a$ 截直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的 形状为四边形;
③平面 $a$ 将直四棱柱分割成的上、下两部分的体积之比 为 $3: 1$;
④)平面 $a$ 截直四棱柱 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的 面积为 $7 \sqrt{3}$;
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
在锐角 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c, \triangle A B C$ 的面积为 $\mathrm{S}$, 若 $\sin (A+C)=\frac{2 S}{b^2-a^2}$, 则 $\tan A+\frac{1}{3 \tan (B-A)}$ 的取值范围为
$\text{A.}$ $\left[\frac{2 \sqrt{3}}{3},+\infty\right)$
$\text{B.}$ $\left[\frac{2 \sqrt{3}}{3}, \frac{4}{3}\right]$
$\text{C.}$ $\left(\frac{2 \sqrt{3}}{3}, \frac{4}{3}\right)$
$\text{D.}$ $\left[\frac{2 \sqrt{3}}{3}, \frac{4}{3}\right)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $\vec{a}, \vec{b}$ 满足: $|\vec{a}|=1, \vec{b}=(-1, \sqrt{3}), \vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{\pi}{3}$, 则 $|\vec{a}-\vec{b}|=$
已知 $f(x)$ 是奇函数, 且当 $x>0$ 时, $f(x)=e^{a x}$, 若 $f\left(\ln \frac{1}{2}\right)=-4$, 则 $a=$
已知等比数列 $\left\{a_n\right\}$ 各项均为正数, 且满足: $a_1>1,2 < a_{101} a_{102}+1 < a_{101}+a_{102}$, 记 $T_n=a_1 a_2 \cdots a_n$, 则使得 $T_n>1$ 的最大正整数 $n$ 为
已知抛物线 $y^2=2 p x(p>0)$, 其焦点为 $F(1,0)$, 准线为 $l$, 过 $F$ 的直线交拋物线于 $A, B$ 两点, 连接 $A O$ ( $O$ 为原点) 交 $l$ 于 $C$, 连接 $B O$ 交 $l$ 于 $D$, 则四边形 $A B C D$ 面 积的最小值为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $f(x)=\sin \left(\frac{\pi x}{4}-\frac{\pi}{6}\right)-2 \cos ^2 \frac{\pi x}{8}+1$.
(I) 求 $f(x)$ 的单调递增区间及其图象的对称轴;
(II) 当 $x \in(0,4)$ 时, 求 $f(x)$ 的值域.
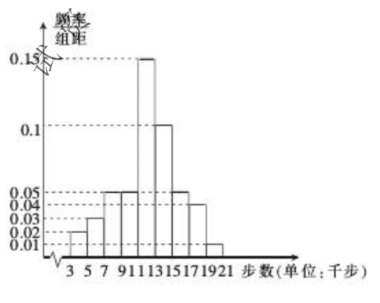
哈尔滨市工会为了解市民日健步走的情况, 从本市市民中随机抽取了 1000 名市民, 利 用手机计步软件统计了他们 3 月 15 日健步的步数, 并将样本数据分为 $[3,5),[5,7),[7,9),
[9,11),[11,13),[13,15),[15,17),[17,19),[19,21]$九组 (单位: 千步),将样本数据绘制成频率分布直方图如图并利用该样本的频率分布估计总体的概率分布.
( I ) 请利用频率分布直方图估计样本平均数 $\bar{x}$ 和众数 $a$;
(II)由频率分布直方图可以认为, 市民日健步步数 $Z$ (单位: 千步) 近似地服从正态分布 $N\left(\mu, \sigma^2\right)$, 其中 $\mu$ 近似为样本平均数 $\bar{x}, \sigma$ 的值已求出约为 $3.64$. 现从哈尔滨全市市民中 随机抽取 5 人, 记其中日健步步数 $Z$ 位于 $(4.88,15.8)$ 的人数为 $X$, 求 $X$ 的数学期望.
参考数据: 若 $Z \sim N(\mu, \sigma)$, 则 $P(\mu-\sigma < Z < \mu+\sigma)=0.6827$,
$$
P(\mu-2 \sigma < Z < \mu+2 \sigma)=0.9545
$$
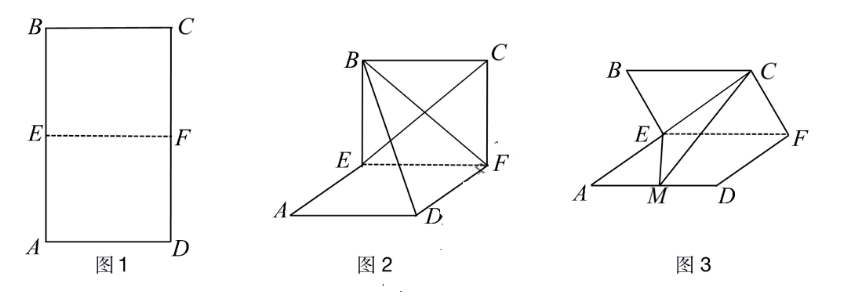
如图 1, 矩形 $A B C D$, 点 $E, F$ 分别是线段 $A B, C D$ 的中点, $A B=4, A D=2$, 将 矩形 $A B C D$ 沿 $E F$ 翻折
(I) 若所成二面角的大小为 $\frac{\pi}{2}$ (如图 2) , 求证: 直线 $C E \perp$ 面 $D B F$;
(II) 若所成二面角的大小为 $\frac{\pi}{3}$ (如图 3), 点 $M$ 在线段 $A D$ 上, 当直线 $B E$ 与面 $E M C$ 所 成角为 $\frac{\pi}{4}$ 时, 求二面角 $D-E M-C$ 的余弦值.
已知函数 $f(x)=\left(\ln x-\frac{1}{2}\right) x^2-6 a(\ln x-1) x, a$ 为常数, $a \in R$
(I) 当 $a=\frac{1}{3}$ 时, 求 $f(x)$ 在 $x=e$ 处的切线方程;
( II ) (i) 讨论函数 $f(x)$ 的单调性;
(ii ) $\forall x \in(e,+\infty)$, 不等式 $f(x)>2 a^2$ 恒成立, 求 $a$ 的取值范围.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{2}}{2}$, 短轴长为 2 .
(I) 求椭圆 $C$ 的标准方程;
( II ) 在圆 $O: x^2+y^2=3$ 上取一动点 $P$ 作椭圆 $C$ 的两条切线, 切点分别记为 $M, N$, ( $P M$ 与 $P N$ 的斜率均存在), 直线 $P M, P N$ 分别与圆 $O$ 相交于异于点 $P$ 的 $A 、 B$ 两 点.
(i) 求证: $|A B|=2 \sqrt{3}$;
(ii) 求 $\triangle O M N$ 面积的取值范围.
在平面直角坐标系 $x o y$ 中, 设曲线 $C_1$ 的参数方程为 $\left\{\begin{array}{l}x=\frac{1}{3} \cos a \\ y=2+\frac{1}{3} \sin a\end{array}\right.$ ( $a$ 为参数), 以坐标 原点为极点, $x$ 轴正半轴为极轴建立极坐标系, 已知曲线 $C_2$ 的极坐标方程为
$$
\rho=\frac{2}{\sqrt{\cos ^2 \theta+4 \sin ^2 \theta}} .
$$
( I ) 求曲线 $C_1$ 的普通方程与曲线 $C_2$ 的直角坐标方程;
(II) 设 $P, Q$ 分别为曲线 $C_1$ 与 $C_2$ 上的动点, 求 $P Q$ 的最大值.
已知函数 $f(x)=|4 x-3|+|4 x+5|$.
(I) 求不等式 $f(x)>14$ 的解集;
(II) 设 $m, n \in \mathbf{R}_{+}$, 且 $m+2 n=3$, 求证: $2^{\sqrt{m}} \cdot 2^{\sqrt{2 n+1}} < f(x)$.