单选题 (共 8 题 ),每题只有一个选项正确
已知全集 $U=A \cup B=\{x \in N \mid 0 \leqslant x \leqslant 10\}, A \cap\left(\complement_U B\right)=\{1,3,5,7\}$, 则集合 $B=(\quad)$
$\text{A.}$ 6
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 不确定
已知 $\mathrm{i}$ 是虚数单位, $\mathrm{i}-1$ 是关于 $x$ 的方程 $x^2+p x+q=0(p, q \in \mathbf{R})$ 的一个根,则 $p+q=$
$\text{A.}$ 4
$\text{B.}$ -4
$\text{C.}$ 2
$\text{D.}$ -2
已知函数 $f(x)$ 满足 $f(-x)-f(x)=0$, 且在 $[0,+\infty)$ 上单调递减, 对于实数 $a, b$, 则 “ $a^2 < b^2$ ” 是 “ $f(a)>$ $f(b)$ ” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
图 1 是蜂房正对着蜜蜂巢穴开口的截面图, 它是由许多个正六边形互相紧挨在一起构成. 可以看出蜂房的底部是由三个大小相同的菱形组成, 且这三个菱形不在一个平面上. 研究表明蜂房底部的菱形相似于菱形十二面体的表面菱形, 图 2 是一个菱形十二面体, 它是由十二个相同的菱形围成的几何体,也可以看作正方体的各个正方形面上扣上一个正四棱椎 (如图 3), 且平面 $A B C D$ 与平面 $A T B S$ 的夹角为 $45^{\circ}$,则 $\cos \angle A S B=$
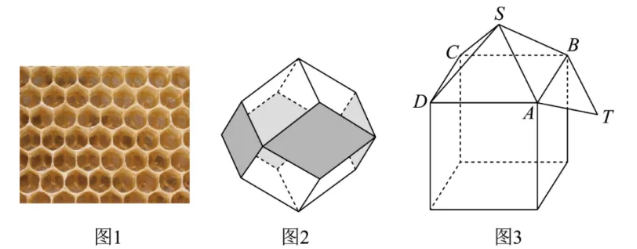
$\text{A.}$ $\frac{\sqrt{2}}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{2 \sqrt{2}}{3}$
在 $\triangle A B C$ 中, 角 $A$ 为 $\frac{\pi}{3}$, 角 $A$ 的平分线 $A D$ 交 $B C$ 于点 $D$, 已知 $A D=2 \sqrt{3}$, 且 $\lambda \overrightarrow{A B}=\overrightarrow{A D}-\frac{1}{3} \overrightarrow{A C}(\lambda \in R)$,则 $\overrightarrow{A B} \cdot \overrightarrow{A D}=$
$\text{A.}$ 1
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ 9
$\text{D.}$ $\frac{3 \sqrt{3}}{2}$
有甲、乙等五人到三家企业去应聘, 若每人至多被一家企业录用, 每家企业至少录用其中一人且甲、乙两人不能被同一家企业录用,则不同的录用情况种数是
$\text{A.}$ 60
$\text{B.}$ 114
$\text{C.}$ 278
$\text{D.}$ 336
设椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 直线 $l$ 过点 $F_1$. 若点 $F_2$ 关于 $l$ 的对称点 $P$恰好在椭圆 $C$ 上, 且 $\overrightarrow{F_1 P} \cdot \overrightarrow{F_1 F_2}=\frac{1}{2} a^2$, 则 $C$ 的离心率为
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{5}$
已知正数 $a, b, c$ 满足 $\mathrm{e}^a=b=\ln c$, $\mathrm{e}$ 为自然对数的底数,则下列不等式一定成立的是
$\text{A.}$ $a+c < 2 b$
$\text{B.}$ $a+c>2 b$
$\text{C.}$ $a c < b^2$
$\text{D.}$ $a c>b^2$
多选题 (共 3 题 ),每题有多个选项正确
一口袋中有除颜色外完全相同的 3 个红球和 2 个白球, 从中无放回的随机取两次,每次取 1 个球,记事件 $A_1$ : 第一次取出的是红球; 事件 $A_2$ : 第一次取出的是白球;事件 $B$ :取出的两球同色;事件 $C$ :取出的两球中至少有一个红球,则
$\text{A.}$ 事件 $A_1, A_2$ 为互斥事件
$\text{B.}$ 事件 $B, C$ 为独立事件
$\text{C.}$ $P(B)=\frac{2}{5}$
$\text{D.}$ $P\left(C \mid A_2\right)=\frac{3}{4}$
已知等比数列 $\left\{a_n\right\}$ 的公比为 $q$, 其前 $n$ 项的积为 $T_n$, 且满足 $a_1>1, a_{99} a_{100}-1>0, \frac{a_{99}-1}{a_{100}-1} < 0$, 则
$\text{A.}$ $0 < q < 1$
$\text{B.}$ $a_{99} a_{101}-1 < 0$
$\text{C.}$ $T_{100}$ 的值是 $T_n$ 中最大的
$\text{D.}$ 使 $T_n>1$ 成立的最大正整数数 $n$ 的值为 198
在长方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $A B=A A_1=2, A D=1, E$ 为 $A_1 B_1$ 的中点, 点 $P$ 满足 $\overrightarrow{D P}=\lambda \overrightarrow{D B_1}(0 < \lambda$ $ < 1$ ), 则
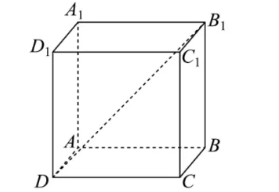
$\text{A.}$ 若 $M$ 为 $A_1 D$ 的中点, 则三梭椎 $P-B E M$ 体积为定值
$\text{B.}$ 存在点 $P$ 使得 $A P \perp B E$
$\text{C.}$ 当 $\lambda=\frac{2}{3}$ 时,平面 $P B C$ 截长方体 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的面积为 $\sqrt{5}$
$\text{D.}$ 若 $Q$ 为长方体 $A B C D-A_1 B_1 C_1 D_1$ 外接球上一点, $\lambda=2$, 则 $Q E+Q P$ 的最小值为 $\sqrt{14}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
若直线 $a x-b y+2=0(a>0, b>0)$ 被圆 $x^2+y^2+2 x-4 y+1=0$ 所截得的弦长为 4 , 则 $\frac{2}{a}+\frac{3}{b}$ 的最小值为
已知函数 $f(x)=2 \sin \left(\omega x+\frac{\pi}{4}\right)(\omega>0)$ 在区间 $[-1,1]$ 上的值域为 $[m, n]$, 且 $n-m=3$, 则 $\omega$ 的值为
正整数 $a 、 b$ 满足 $2 < 2 a < b$, 若关于 $x 、 y$ 的方程组 $\left\{\begin{array}{l}y=-2 x+2024, \\ y=|x-1|+|x-a|+|x-b|\end{array}\right.$ 有且只有一组解, 则 $a$ 的最大值为
已知数列 $\left\{a_n\right\}$ 中, $a_2=1$, 设 $S_n$ 为 $\left\{a_n\right\}$ 前 $n$ 项和, $2 S_n=n a_n$.
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=\frac{\sin 1}{\cos \left(a_n+1\right) \cos \left(a_{n+1}+1\right)}$, 求数列 $\left\{b_n\right\}$ 的前 $n$ 项和 $T_n$
某兴趣小组为研究一种地方性疾病与当地居民的卫生习惯 (卫生习惯分为良好和不够良好两类) 的关系, 设 $A=$ “患有地方性疾病”, $B=$ “卫生习惯良好”. 据临床统计显示, $P(A \mid \bar{B})=\frac{3}{4}, P(B \mid \bar{A})=\frac{12}{13}$,该地人群中卫生习惯良好的概率为 $\frac{4}{5}$.
(1) 求 $P(A)$ 和 $P(A \mid B)$;
(2) 为进一步验证 (1) 中的判断,该兴趣小组用分层抽样的方法在该地抽取了一个容量为 $m\left(m \in N^*\right)$ 的样本, 利用独立性检验, 计算得 $\chi^2=2.640$. 为提高检验结论的可靠性, 现将样本容量调整为原来的 $k\left(k \in N^*\right)$ 倍, 使得能有 $99.9 \%$ 的把握肯定 (1) 中的判断, 试确定 $k$ 的最小值.
附表及公式: $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}, n=a+b+c+d$

已知 $f(x)=x^2-2 m \ln x-1$.
(1) 若 $f(x)$ 的最小值为 0 , 求 $m$ 的值;
(2) 若 $a e^{x^2-1}-1 \geqslant 2 \ln x-\ln a$ 恒成立,求实数 $a$ 的取值范围.
已知 $M, N$ 为椭圆 $C_1: \frac{x^2}{a^2}+y^2=1(a>0)$ 和双曲线 $C_2: \frac{x^2}{a^2}-y^2=1$ 的公共顶点, $\mathrm{e}_1, \mathrm{e}_2$ 分别为 $C_1$ 和 $C_2$ 的离心率.
(1) 若 $\mathrm{e}_1 \mathrm{e}_2=\frac{\sqrt{15}}{4}$.
(i) 求 $C_2$ 的渐近线方程;
(ii) 过点 $G(4,0)$ 的直线 $l$ 交 $C_2$ 的右支于 $A, B$ 两点, 直线 $M A, M B$ 与直线 $x=1$ 相交于 $A_1, B_1$ 两点, 记 $A, B, A_1, B_1$ 的坐标分别为 $\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right),\left(x_4, y_4\right)$, 求证: $\frac{1}{y_1}+\frac{1}{y_2}=\frac{1}{y_3}+\frac{1}{y_4}$;
(2) 从 $C_2$ 上的动点 $P\left(x_0, y_0\right)\left(x_0 \neq \pm a\right)$ 引 $C_1$ 的两条切线, 经过两个切点的直线与 $C_2$ 的两条渐近线围成三角形的面积为 $S$, 试判断 $S$ 是否为定值? 若是, 请求出该定值; 若不是, 请说明理由.
对于空间向量 $\vec{m}=(a, b, c)$, 定义 $\|\vec{m}\|=\max \{|a|,|b|,|c|\}$, 其中 $\max \{x, y, z\}$ 表示 $x, y, z$ 这三个数的最大值.
(1) 已知 $\vec{a}=\left(6, \frac{11}{2}, 1\right), \vec{b}=\left(x, \frac{1}{2} x,-x\right)$.
①写出 $\|\vec{a}\|$,写出 $\|\vec{b}\|$ (用含 $x$ 的式子表示);
②当 $0 \leqslant x \leqslant 4$, 写出 $\|\vec{a}-\vec{b}\|$ 的最小值及此时 $x$ 的值;
(2) 设 $\vec{a}=\left(x_1, y_1, z_1\right), \vec{b}=\left(x_2, y_2, z_2\right)$, 求证: $\|\vec{a}+\vec{b}\| \leqslant\|\vec{a}\|+\|\vec{b}\|$
(3) 在空间直角坐标系 $O-x y z$ 中, $A(2,0,0), B(0,4,0), C(0,0,6)$, 点 $P$ 是以 $O$ 为球心, 1 为半径的球面上的动点, 点 $Q$ 是 $\triangle A B C$ 内部的动点, 直接写出 $\|\overrightarrow{P Q}\|$ 的最小值及相应的点 $P$ 的坐标.