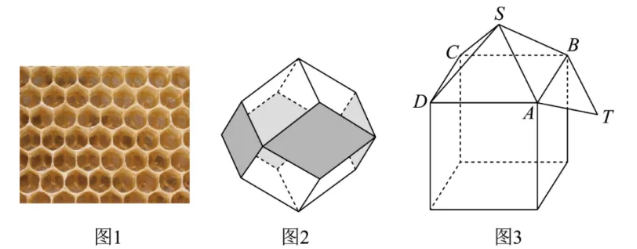
图 1 是蜂房正对着蜜蜂巢穴开口的截面图, 它是由许多个正六边形互相紧挨在一起构成. 可以看出蜂房的底部是由三个大小相同的菱形组成, 且这三个菱形不在一个平面上. 研究表明蜂房底部的菱形相似于菱形十二面体的表面菱形, 图 2 是一个菱形十二面体, 它是由十二个相同的菱形围成的几何体,也可以看作正方体的各个正方形面上扣上一个正四棱椎 (如图 3), 且平面
A.