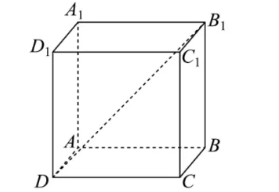
在长方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $A B=A A_1=2, A D=1, E$ 为 $A_1 B_1$ 的中点, 点 $P$ 满足 $\overrightarrow{D P}=\lambda \overrightarrow{D B_1}(0 < \lambda$ $ < 1$ ), 则

A. 若 $M$ 为 $A_1 D$ 的中点, 则三梭椎 $P-B E M$ 体积为定值
B. 存在点 $P$ 使得 $A P \perp B E$
C. 当 $\lambda=\frac{2}{3}$ 时,平面 $P B C$ 截长方体 $A B C D-A_1 B_1 C_1 D_1$ 所得截面的面积为 $\sqrt{5}$
D. 若 $Q$ 为长方体 $A B C D-A_1 B_1 C_1 D_1$ 外接球上一点, $\lambda=2$, 则 $Q E+Q P$ 的最小值为 $\sqrt{14}$