单选题 (共 8 题 ),每题只有一个选项正确
$A=\left\{x \mid x^2-5 x+6 \leq 0\right\}, B=\{x \mid-1 \leq x < 3\}$, 则 $A \cap B=$
$\text{A.}$ $\{x \mid-1 \leq x < 3\}$
$\text{B.}$ $\{x \mid-1 \leq x \leq 3\}$
$\text{C.}$ $\{x \mid 2 \leq x < 3\}$
$\text{D.}$ $\{x \mid 2 \leq x \leq 3\}$
函数 $f(x)=2^x+x^3-9$ 的零点所在区间为
$\text{A.}$ $(0,1)$
$\text{B.}$ $(1,2)$
$\text{C.}$ $(2,3)$
$\text{D.}$ $(3,4)$
设函数 $f(x)=\frac{a-1}{a^x-1}+b(a>0, a \neq 1)$, 则函数 $f(x)$ 的单调性
$\text{A.}$ 与 $a$ 有关, 且与 $b$ 有关
$\text{B.}$ 与 $a$ 无关, 且与 $b$ 有关
$\text{C.}$ 与 $a$ 有关, 且与 $b$ 无关
$\text{D.}$ 与 $a$ 无关, 且与 $b$ 无关
已知等差数列 $\left\{a_n\right\}$, 则 $k=2$ 是 $a_1+a_{11}=a_k+a_{10}$ 成立的 ________ 条件
$\text{A.}$ 充要
$\text{B.}$ 充分不必要
$\text{C.}$ 必要不充分
$\text{D.}$ 既不充分也不必要
已知直线 $a, m, n, l$, 且 $m, n$ 为异面直线, $m \perp$ 平面 $\alpha, n \perp$ 平面 $\beta$. 若 $l$ 满足 $l \perp m$, $l \perp n$, 则下列说法中正确的是
$\text{A.}$ $l / / \alpha$
$\text{B.}$ $l \perp \beta$
$\text{C.}$ 若 $\alpha \cap \beta=a$, 则 $a / / l$
$\text{D.}$ $\alpha \perp \beta$
已知 $\vec{e}_1, \overrightarrow{e_2}$ 是单位向量, 且它们的夹角是 $60^{\circ}$. 若 $\vec{a}=\overrightarrow{e_1}+2 \overrightarrow{e_2}, \vec{b}=\lambda \overrightarrow{e_1}-\overrightarrow{e_2}$, 且 $|\vec{a}|=|\vec{b}|$, 则 $\lambda=$
$\text{A.}$ 2
$\text{B.}$ -2
$\text{C.}$ 2 或 -3
$\text{D.}$ 3 或 -2
函数 $f(x)=\frac{5 \sin x}{\mathrm{e}^{|x|}}+x \cos x$ 在 $[-2 \pi, 2 \pi]$ 上的图象大致为
$\text{A.}$  $\text{B.}$
$\text{B.}$ 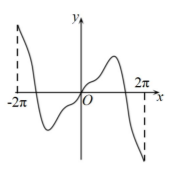 $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 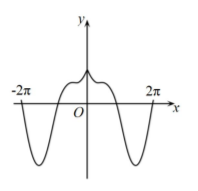
设实数 $x, y$ 满足 $x>\frac{3}{2}, y>3$, 不等式 $k(2 x-3)(y-3) \leq 8 x^3+y^3-12 x^2-3 y^2$ 恒成立, 则实数 $k$ 的最大值为
$\text{A.}$ 12
$\text{B.}$ 24
$\text{C.}$ $2 \sqrt{3}$
$\text{D.}$ $4 \sqrt{3}$
多选题 (共 3 题 ),每题有多个选项正确
已知复数 $z_1, z_2$, 则下列结论正确的有
$\text{A.}$ $z_1^2=\overline{z_1^2}$
$\text{B.}$ $\overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z_2}$
$\text{C.}$ $\left|z_1 z_2\right|=\left|z_1\right| \cdot\left|z_2\right|$
$\text{D.}$ $\left|z_1+z_2\right|=\left|z_1\right|+\left|z_2\right|$
已知 $f(x), g(x)$ 的定义域为 $R$, 且 $f(x)+g(1-x)=a(a \neq 0), g(1+x)=g(1-x)$,若 $f(x+2)$ 为奇函数, 则
$\text{A.}$ $g(x)$ 关于 $x=1$ 对称
$\text{B.}$ $g(x)$ 为奇函数
$\text{C.}$ $f(2)=0$
$\text{D.}$ $f(x)$ 为偶函数
已知 $O$ 为坐标原点, 曲线 $\Gamma:\left(x^2+y^2\right)^2=a y\left(3 x^2-y^2\right), a>0, P\left(x_0, y_0\right)$ 为曲线 $\Gamma$ 上动点, 则
$\text{A.}$ 曲线 $\Gamma$ 关于 $y$ 轴对称
$\text{B.}$ 曲线 $\Gamma$ 的图象具有 3 条对称轴
$\text{C.}$ $y_0 \in\left[-a, \frac{9}{16} a\right]$
$\text{D.}$ $|O P|$ 的最大值为 $\sqrt{3} a$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $a \sin 2 B-\frac{c}{2} \sin 2 A=a \sin A \cos C$. 则角 $B=$
镇海中学举办大观红楼知识竞赛, 该比赛为擂台赛, 挑战者向守擂者提出挑战, 两人轮流答题, 直至一方答不出或答错, 则另一方自动获胜, 挑战者先答题, 守擂者和挑战者每次答对问题的概率都是 $\frac{1}{2}$, 每次答题互相独立, 则挑战者最终获胜的概率为
在四面体 $P-A B C$ 中, $B P \perp P C, \angle B A C=60^{\circ}$, 若 $B C=2$, 则四面体 $P-A B C$ 体积的最大值是 ________ , 它的外接球表面积的最小值为 ________
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 向量 $\vec{m}=(b-a, c), \vec{n}=(\sin B-\sin C, \sin A+\sin B)$, 且 $\vec{m} / / \vec{n}$.
(1) 求 $A$;
(2) 若 $\triangle A B C$ 的外接圆半径为 2 , 且 $\cos B \cos C=-\frac{1}{6}$, 求 $\triangle A B C$ 的面积.
已知 $T_n$ 为正项数列 $\left\{a_n\right\}$ 的前 $n$ 项的乘积, 且 $a_1=3, T_n^2=a_n^{n+1}$, 数列 $\left\{b_n\right\}$ 满足 $b_n=k a_n-n$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若数列 $\left\{b_n\right\}$ 为递增数列, 求实数 $k$ 的取值范围;
某款游戏预推出一项皮肤抽卡活动, 玩家每次抽卡需要花费 10 元, 现有以下两种方案.方案一: 没有保底机制, 每次抽卡抽中新皮肤的概率为 $p_1$; 方案二: 每次抽卡抽中新皮肤的概率为 $p_2$, 若连续 99 次未抽中, 则第 100 次必中新皮肤. 已知 $0 < p_2 < p_1 < 1$, 玩家按照一、二两种方案进行抽卡, 首次抽中新皮肤时的累计花费为 $X, Y$ (元).
(1) 求 $X, Y$ 的分布列;
(2) 求 $E(X)$;
(3) 若 $p_1=2 p_2=0.02$, 根据花费的均值从游戏策划角度选择收益较高的方案.
$0.99^{100} \approx 0.37 $
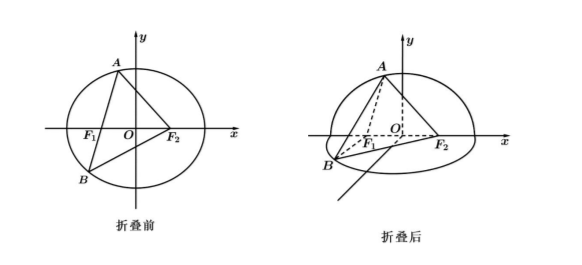
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1 、 F_2$, 离心率为 $\frac{1}{2}$, 经过点 $F_1$ 且倾斜角为 $\theta\left(0 < \theta < \frac{\pi}{2}\right)$ 的直线 $l$ 与椭圆交于 $\mathrm{A} 、 B$ 两点 (其中点 $\mathrm{A}$ 在 $x$ 轴上方), $\triangle A B F_2$ 的周长为 8.
(1) 求椭圆 $C$ 的标准方程;
(2) 如图, 将平面 $x O y$ 沿 $x$ 轴折叠, 使 $y$ 轴正半轴和 $x$ 轴所确定的半平面 (平面 $A F_1 F_2$ ) 与 $y$ 轴负半轴和 $x$ 轴所确定的半平面 (平面 $B F_1 F_2$ ) 互相垂直.
①若 $\theta=\frac{\pi}{3}$, 求三棱椎 $A-B F_1 F_2$ 的体积,
② 若 $\theta=\frac{\pi}{3}$, 异面直线 $A F_1$ 和 $B F_2$ 所成角的余弦值;
③ 是否存在 $\theta\left(0 < \theta < \frac{\pi}{2}\right)$, 使得 $\triangle A B F_2$ 折叠后的周长为与折叠前的周长之比为 $\frac{15}{16}$ ? 若存在, 求 $\tan \theta$ 的值; 若不存在, 请说明理由.
在几何学常常需要考虑曲线的弯曲程度, 为此我们需要刻画曲线的弯曲程度.考察如图所示的光滑曲线 $C: y=f(x)$ 上的曲线段 $\overparen{A B}$, 其弧长为 $\Delta s$, 当动点从 $A$ 沿曲线段$\overparen{A B}$ 运动到 $B$ 点时, $A$ 点的切线 $l_A$ 也随着转动到 $B$ 点的切线
$l_B$, 记这两条切线之间的夹角为 $\Delta \theta$ (它等于 $l_B$ 的倾斜角与 $l_A$的倾斜角之差).显然, 当弧长固定时, 夹角越大, 曲线的弯曲程度就越大; 当夹角固定时, 弧长越小则弯曲程度越大,因此可以定义 $\bar{K}=\left|\frac{\Delta \theta}{\Delta s}\right|$ 为曲线段 $\overparen{A B}$ 的平均曲率; 显然当 $B$ 越接近 $A$, 即 $\Delta s$ 越小, $\bar{K}$ 就越能精确刻画曲线 $C$ 在点 $A$ 处的弯曲程度, 因此定义 $K=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \theta}{\Delta s}\right|=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}$ (若极限存在) 为曲线 $C$ 在点 $A$ 处的曲率. (其中 $y^{\prime}, y^{\prime \prime}$ 分别表示 $y=f(x)$ 在点 $A$ 处的一阶、二阶导数)
(1) 求单位圆上圆心角为 $60^{\circ}$ 的圆弧的平均曲率;
(2) 求椭圆 $\frac{x^2}{4}+y^2=1$ 在 $\left(\sqrt{3}, \frac{1}{2}\right)$ 处的曲率;
(3) 定义 $\varphi(y)=\frac{2 \sqrt{2}\left|y^{\prime \prime}\right|}{\left(1+y^{\prime}\right)^3}$ 为曲线 $y=f(x)$ 的 “柯西曲率”. 已知在曲线 $f(x)=x \ln x-2 x$ 上存在两点 $P\left(x_1, f\left(x_1\right)\right)$ 和 $Q\left(x_2, f\left(x_2\right)\right)$, 且 $P, Q$ 处的 “柯西曲率” 相同, 求 $\sqrt[3]{x_1}+\sqrt[3]{x_2}$ 的取值范围
