已知椭圆
(1) 求椭圆
(2) 如图, 将平面
①若
② 若
③ 是否存在
(1) 求椭圆
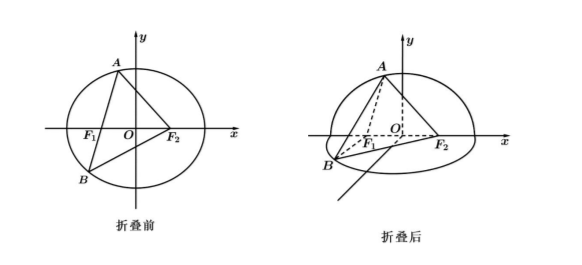
(2) 如图, 将平面
①若
② 若
③ 是否存在
