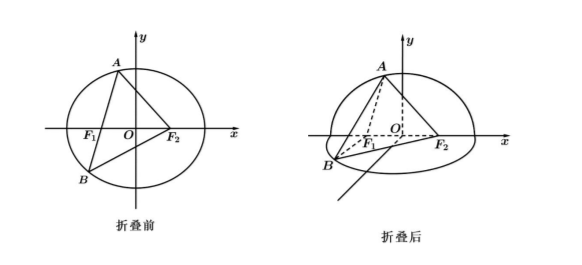
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1 、 F_2$, 离心率为 $\frac{1}{2}$, 经过点 $F_1$ 且倾斜角为 $\theta\left(0 < \theta < \frac{\pi}{2}\right)$ 的直线 $l$ 与椭圆交于 $\mathrm{A} 、 B$ 两点 (其中点 $\mathrm{A}$ 在 $x$ 轴上方), $\triangle A B F_2$ 的周长为 8.
(1) 求椭圆 $C$ 的标准方程;
(2) 如图, 将平面 $x O y$ 沿 $x$ 轴折叠, 使 $y$ 轴正半轴和 $x$ 轴所确定的半平面 (平面 $A F_1 F_2$ ) 与 $y$ 轴负半轴和 $x$ 轴所确定的半平面 (平面 $B F_1 F_2$ ) 互相垂直.

①若 $\theta=\frac{\pi}{3}$, 求三棱椎 $A-B F_1 F_2$ 的体积,
② 若 $\theta=\frac{\pi}{3}$, 异面直线 $A F_1$ 和 $B F_2$ 所成角的余弦值;
③ 是否存在 $\theta\left(0 < \theta < \frac{\pi}{2}\right)$, 使得 $\triangle A B F_2$ 折叠后的周长为与折叠前的周长之比为 $\frac{15}{16}$ ? 若存在, 求 $\tan \theta$ 的值; 若不存在, 请说明理由.