单选题 (共 8 题 ),每题只有一个选项正确
已知全集 $U=\{0,1,2,3,4,5,6,7,8\}$, 集合 $A=\{x \in N \mid x < 5\}, B=\{1,3,5,7,8\}$,则图中阴影部分所表示的集合为
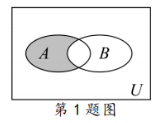
$\text{A.}$ $\{0,2,4\}$
$\text{B.}$ $\{2,4\}$
$\text{C.}$ $\{0,4\}$
$\text{D.}$ $\{2,4,6\}$
已知复数 $z$ 在复平面内的对应点为 $(1,1)$, 则 $z+\frac{1}{z}$ 的虚部为
$\text{A.}$ $\frac{1}{2} \mathrm{i}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{3}{2} \mathrm{i}$
已知 $x \in R$, 则 “ $x^3>8$ ” 是 “ $|x|>2$ ” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
某地投资 $a$ 亿元进行基础建设, $t$ 年后产生的社会经济效益为 $f(t)=a e^{\lambda t}$ 亿元, 若该地投资基础建设 4 年后产生的社会经济效益是投资额的 2 倍, 且再过 $t_1$ 年, 该项投资产生的社会经济效益是投资额的 8 倍, 则 $t_1=$
$\text{A.}$ 4
$\text{B.}$ 8
$\text{C.}$ 12
$\text{D.}$ 16
如图, $\mathrm{ABCD}$ 是边长 2 的正方形, $\mathrm{P}$ 为半圆弧 $\mathrm{BC}$ 上的动点 (含端点)则 $\overrightarrow{A B} \cdot \overrightarrow{A P}$ 的取值范围为

$\text{A.}$ $[2,6]$
$\text{B.}$ $[2,3]$
$\text{C.}$ $[4,6]$
$\text{D.}$ $[4,8]$
已知函数 $f(x)=2 \sin x-\mathrm{e}^x+\mathrm{e}^{-x}$, 则关于 $x$ 的不等式 $f\left(x^2-4\right)+f(3 x) < 0$ 的解集为
$\text{A.}$ $(-4,1)$
$\text{B.}$ $(-1,4)$
$\text{C.}$ $(-\infty,-4) \cup(1,+\infty)$
$\text{D.}$ $[-1,4]$
从集合 $S=\{x \in N \mid 1 \leq x \leq 10\}$ 中任取 3 个不同的数, 它们的和能被 3 整除的概率为
$\text{A.}$ $\frac{3}{10}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{41}{120}$
$\text{D.}$ $\frac{7}{20}$
$f(x)=2 e^x-5 x^2$ 的零点的个数为
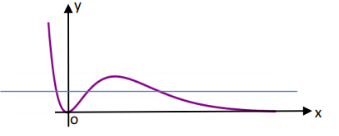
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
多选题 (共 4 题 ),每题有多个选项正确
国际跳水比赛一共有八个评委现场打分, 若八位评委给某个选手的打分分别为 $x_1, x_2, \cdots, x_8$, 记这组数据的平均分, 中位数, 方差, 极差分别为 $\bar{x} 、 z 、 s^2 、 j$, 去掉这组数据的一个最高分和一个最低分后, 其平均数, 中位数, 方差, 极差分别为 $\bar{x}^{\prime} 、 z^{\prime} 、\left(s^{\prime}\right)^2 、 j^{\prime}$, 则下列判断中一定正确的是
$\text{A.}$ $\bar{x} \leq \bar{x}^{\prime}$
$\text{B.}$ $z=z^{\prime}$
$\text{C.}$ $\left(s^{\prime}\right)^2 \leq s^2$
$\text{D.}$ $j^{\prime} \leq j$
在平面直角坐标系中, 已知角 $\alpha$ 的顶点与坐标原点重合, 始边与 $x$ 轴的非负半轴重合, 终边经过点 $\left(-\sin \frac{\pi}{3}, \cos \frac{\pi}{3}\right), f(x)=\cos \alpha \sin 2 x-\sin \alpha \cos 2 x$ 则下列结论正确的是
$\text{A.}$ $1-\cos 2 \alpha=\frac{1}{2}$
$\text{B.}$ $x=\frac{2 \pi}{3}$ 是 $y=f(x)$ 的一条对称轴
$\text{C.}$ 将函数 $y=f(x)$ 图象上的所有点向左平移 $\frac{5 \pi}{6}$ 个单位长度, 所得到的函数解析式为 $y=\sin 2 \mathrm{x}$
$\text{D.}$ $y=f(x)$ 在 $\left(0, \frac{4 \pi}{3}\right)$ 内恰有 3 个零点
如图, 已知二面角 $\alpha-l-\beta$ 的棱 $l$ 上有 $A, B$ 两点, $C \in \alpha, A C \perp l, D \in \beta, B D \perp l$, 且 $A C=A B=B D=1$, 则下列说法正确的是

$\text{A.}$ $\overrightarrow{C D} \cdot \overrightarrow{A B}=1$
$\text{B.}$ 当二面角 $\alpha-l-\beta$ 的大小为 $60^{\circ}$ 时, $C D$ 与平面 $\beta$ 所成的角为 $30^{\circ}$
$\text{C.}$ 若 $C D=\sqrt{3}$, 则四面体 $A B C D$ 的体积为 $\frac{1}{12}$
$\text{D.}$ 若 $C D=\sqrt{2}$, 则二面角 $C-B D-A$ 的余弦值为 $\frac{2 \sqrt{7}}{7}$
如图, 双曲线 $\mathrm{C}: x^2-y^2=a^2$ 的左右顶点为 $\mathrm{A}, \mathrm{B}, \mathrm{P}$ 为 $\mathrm{C}$ 右支上一点 (不包含顶点), $\angle P A B=\alpha, \angle P B A=\beta, \angle A P B=\gamma$, 直线 $l$ 与 $\mathrm{C}$ 的渐近线交于 $\mathrm{F} 、 \mathrm{G}, \mathrm{M}$ 为线段 $\mathrm{FG}$ 的中点, 则

$\text{A.}$ 双曲线 $\mathrm{C}$ 的离心率为 $e=\sqrt{2}$
$\text{B.}$ $\mathrm{P}$ 到两条渐近线的距离之积为 $a^2$
$\text{C.}$ $\tan \alpha+\tan \beta+2 \tan \gamma=0$
$\text{D.}$ 若直线 $l$ 与 $\mathrm{OM}$ 的斜率分别为 $k_1, k_2$, 则 $k_1 k_2=1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$(2 x-1)^5$ 展开式中 $x^2$ 项的系数是
已知 $x, y>0, x+4 y-x y+5=0$, 则 $x y$ 的最小值为
已知 $\mathrm{F}$ 是抛物线 $\mathrm{C}: y^2=8 x$ 的焦点, 过抛物线 $\mathrm{C}$ 上一点 $\mathrm{M}$ 作其准线的垂线, 垂足为 $\mathrm{N}$, 若 $\angle N F M=\frac{\pi}{3}$,则 $M$ 点的横坐标为
对 $\forall x_1, x_2$, 当 $1 < x_1 < x_2 < e$ 时 $\left(\frac{x_2}{x_1}\right)^{x_1 x_2}-\frac{e^{a x_2}}{e^{a x_1}} < 0$, 则 $a$ 的范围为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $a, b, c$ 分别是三角形三个内角 $A, B, C$ 的对边, 已知 $a=5, \sin A=\frac{3}{5}, B-A=\frac{\pi}{2}$
(I) 求 $\cos C$ 的值;
(II) 求 $\triangle A B C$ 的周长.
已知 $\left\{a_n\right\}$ 为等差数列, 公差 $d \neq 0,\left\{a_n\right\}$ 中的部分项 $a_{k_1}, a_{k_2}, \cdots \cdots, a_{k_n}$ 恰为等比数列, 且公比为 $q$,若 $k_1=1, k_2=6, k_3=16$
(I) 求 $q$;
(II) 求数列 $\left\{k_n\right\}$ 的通项公式及其前 $\mathrm{n}$ 项之和.
如图, 平面 $A B C D \perp$ 平面 $A B E$, 点 $E$ 为半圆弧 $A B$ 上异于 $A, B$ 的点, 在矩形 $A B C D$ 中, $A B=4 B C$,设平面 $A B E$ 与平面 $C D E$ 的交线为 $l$.
( I ) 证明: $l / /$ 平面 $A B C D$;
(II) 当 $l$ 与半圆弧 $A B$ 相切时, 求平面 $\mathrm{ADE}$ 与平面 $\mathrm{CDE}$ 的夹角的余弦值.
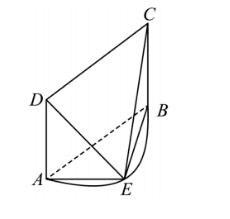
如图, 某人设计了一个类似于高尔顿板的游戏: 将一个半径适当的小球放入如图所示的容器最上方的中间入口处, 小球将自由下落, 小球在下落的过程中, 将 3 次遇到黑色障碍物, 已知小球每次遇到黑色障碍物时, 向左、右两边下落的概率都是 $\frac{1}{2}$, 最后落入 $A$ 袋或 $B$ 袋中. 一次游戏中小球落入 $\mathrm{A}$ 袋记 1 分, 落入 $\mathrm{B}$ 袋记 2 分, 游戏可以重复进行. 游戏过程中累计得 $\mathrm{n}$ 分的概率为 $P_n$.
( I ) 求 $P_1, P_2, P_3$.
( II ) 写出 $P_n$ 与 $P_{n-1}$ 之间的递推关系, 并求出 $P_n$ 的通项公式.
设动圆 $\mathrm{M}$ 与圆 $F_1:(x+1)^2+y^2=\frac{1}{4}$ 外切, 与圆 $F_2:(x-1)^2+y^2=\frac{49}{4}$ 内切.
( I ) 求点 $M$ 的轨迹 $\mathrm{C}$ 的方程;
(II) 过点 $F_2$ 且不与 $\mathrm{x}$ 轴垂直的直线 $l$ 交轨迹 $\mathrm{C}$ 于 $\mathrm{A}, \mathrm{B}$ 两点, 点 $\mathrm{A}$ 关于 $\mathrm{x}$ 轴的对称点为 $A^{\prime}, Q$ 为 $\triangle A A^{\prime} B$的外心, 试探究 $\frac{\left|Q F_2\right|}{|A B|}$ 是否为定值, 若是, 求出该定值; 若不是, 请说明理由.
已知函数 $f(x)=\ln (m x), m$ 是大于 0 的常数. 记曲线 $y=f(x)$ 在点 $\left(x_1, f\left(x_1\right)\right)$ 处的切线为 $l$, $l$ 在 $x$ 轴上的截距为 $x_2, x_2>0$
(I) 当 $x_1=\frac{1}{e}, m=1$ 时求切线 $l$ 的方程;
(II) 证明: $\left|x_1-\frac{1}{m}\right| \geq\left|x_2-\frac{1}{m}\right|$.