单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\{x \mid x>5\}, B=\left\{x \mid x^2-(a+1) x+a < 0\right\}$, 若 $A \cap B=\varnothing$, 则 $a$ 的取值范围为
$\text{A.}$ $(-\infty, 5]$
$\text{B.}$ $[5,+\infty)$
$\text{C.}$ $(-\infty, 5)$
$\text{D.}$ $(5,+\infty)$
若 $(1-2 i)(z-i)=5$, 则 $|z|=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $\sqrt{10}$
在 $\triangle A B C$ 中, 点 $D$ 是边 $B C$ 上一点, 若 $\overrightarrow{A D}=x \overrightarrow{A B}+y \overrightarrow{A C}$, 则 $\frac{2 x+5 y}{x y}$ 的最小值为 ()
$\text{A.}$ $7-2 \sqrt{10}$
$\text{B.}$ $7+2 \sqrt{10}$
$\text{C.}$ $-2 \sqrt{10}$
$\text{D.}$ 7
将函数 $f(x)=8 \sin x$ 图象向右平移 $\frac{\pi}{8}$ 后, 再将所得图象上各点横坐标扩大为原来的 4 倍, 得到 $g(x)$ 的图象, 若方程 $g(x)=4$ 在 $[0,8 \pi]$ 内有两不等实根 $\alpha, \beta$, 则 $\cos \left(\alpha+\beta+\frac{\pi}{6}\right)=(\quad)$
$\text{A.}$ $-\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ -1
$\text{D.}$ $-\frac{1}{2}$
已知正四棱台下底面边长为 $4 \sqrt{2}$, 若内切球的休积为 $\frac{32}{3} \pi$, 则其外接球表面积为 ( )
$\text{A.}$ $49 \pi$
$\text{B.}$ $56 \pi$
$\text{C.}$ $65 \pi$
$\text{D.}$ $130 \pi$
设数列 $\left\{a_n\right\}$ 的前 $n$ 面和为 $S_n$, 若 $a_{n+1}=2 \sqrt{S_n}+1$, 且 $a_1=1$, 则 ( )
$\text{A.}$ $a_5 < 5$
$\text{B.}$ $a_5>10$
$\text{C.}$ $S_{100}>1000$
$\text{D.}$ $S_{100} < 10000$
已知函数 $f(x)$ 的定义域为 R , 且 $f(x+3)$ 为奇函数, $f(2-x)$ 为偶函数, 记 $f(x)$ 的导函数为 $f^{\prime}(x)$,
则下列函数为奇函数的是 ( )
$\text{A.}$ $f(x-1)$
$\text{B.}$ $f^{\prime}(-x+3)$
$\text{C.}$ $f(x+2)$
$\text{D.}$ $f(x)$
设曲线 $D$ 的方程为 $a x^3+b y^3=x y$ ( $a, b$ 为系数), 则
$\text{A.}$ 曲线 $D$ 一定经过第一象限
$\text{B.}$ 当 $a=0$, 曲线 $D$ 可能为抛物线
$\text{C.}$ 曲线 $D$ 一定经过第三象限
$\text{D.}$ 当 $a=b$, 曲线 $D$ 一定关于直线 $y=x$ 对称
多选题 (共 3 题 ),每题有多个选项正确
设 $A, B$ 是非空的实数集, 若 $f: A \rightarrow B$, 则 ( )
$\text{A.}$ 函数 $f(x)$ 的定义域为 $A$
$\text{B.}$ 函数 $f(x)$ 的值域为 $B$
$\text{C.}$ 函数 $f(x)=a x^3+b x$ 值域为 R
$\text{D.}$ 函数 $f(x)=x^3-3 x^2+3 x$ 无极值
已知一组数据的平均数、中位数、众数依次成等差数列, 现在丢失了其中一个数据, 另外六个数据分别是 7, 9, 10, 7, 15, 7. 将丢失数据的所有可能值从小到大排列成数列 $\left\{a_n\right\}$, 记 $X=\left\{a_1, a_2, \cdots, a_n\right\}$,
$\text{A.}$ $E(X)=8$
$\text{B.}$ $D(X)=130$
$\text{C.}$ $\left\{a_n\right\}$ 是等差数列
$\text{D.}$ $\left\{a_n\right\}$ 是等比数列
若平面点集 $M$ 满足: 任意点 $(x, y) \in M$, 存在 $t \in(0,+\infty)$, 都有 $(t x, t y) \in M$, 则称该点集 $M$ 是 $t$ 阶聚合点集. 下列命题为真命题的是 ( )
$\text{A.}$ 若 $M=\{(x, y) \mid x \geq y\}$, 则 $M$ 是 3 阶聚合点集
$\text{B.}$ 存在 $M$ 对任意正数 $t$, 使 $M$ 不是 $t$ 阶聚合点集
$\text{C.}$ 若 $M=\left\{(x, y) \left\lvert\, \frac{x^2}{4}+y^2=1\right.\right\}$, 则 $M$ 不是 $\frac{1}{3}$ 阶聚合点集
$\text{D.}$ " $t \in[1,+\infty)$ " 是 " $M=\left\{(x, y) \mid y^2 \geq x\right\}$ 是 $t$ 阶聚合点集" 的充要条件
填空题 (共 3 题 ),请把答案直接填写在答题纸上
正八面体中, 以其顶点为顶点的三棱锥的个数为 $\qquad$ (用数字作答).
将一装有适量水的圆柱容器斜靠在墙面, 已知墙面与水平地面垂直, 若圆柱轴线与水平地面所成角为 $60^{\circ}$, 则液面所呈概圆的离心率为
已知函数 $f(x)=\ln \left|\frac{1}{x}-\frac{e}{2}\right|$, 则曲线 $y=f(x)$ 的对称中心为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 已知 $2 \sin A+3 \cos B \cos C=4$.
(1) 证明: $b=c$ ;
(2) 是否存在 $\triangle A B C$ 内一点 $D$ 使得 $\overrightarrow{D A}+\overrightarrow{D B}+\overrightarrow{D C}=\overrightarrow{0}$ 且 $\overrightarrow{D B} \cdot \overrightarrow{D C}=0$ ? 若存在, 求出 $\frac{B D}{C D}$ 的值; 若不存在, 说明理由.
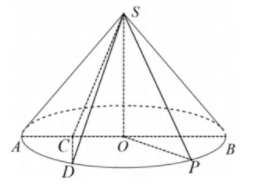
如图, 在圆锥 $S O$ 中, 高 $S O=3$, 底面圆 $O$ 的直径 $A B=5, C$ 是 $O A$ 的中点, 点 $D$ 在圆 $O$ 上, 平面 $S A B \perp$ 平面 $S C D$.
(1) 证明: $C D \perp A B$;
(2) 若点 $P$ 是圆 $O$ 上动点, 求平面 $S C D$ 与平面 $S O P$ 所成角余弦值的取值范围.
已知函数 $f(x)=x \ln x-a\left(x^2-1\right)$.
(1) 讨论函数 $f(x)$ 的零点个数:
(2) 若 $f(x)$ 有三个零点 $x_1, x_1, x_3$, 求 $\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$ 的取值范围.
为庆祝祖国 75 周年华诞, 某商场决定在国庆期间举行抽奖活动. 盖中装有 5 个除颜色外均相同的小球,其中 2 个是红球, 3 个是黄球. 每位顾客均有一次抽奖机会, 抽奖时从盒中随机取出 1 球, 若取出的是红球,则可领取 "特等奖", 该小球不再放回:若取出的是黄球,则可领取 "参与奖",并将该球放回盒中.
(1) 在第 2 位顾客中 "参与奖" 的条件下, 第 1 位顾客中 "特等奖" 的概率;
(2) 记 $p_{n-1}$ 为第 $n$ 个顾客参与后后来参与的顾客不再有机会中 "特等奖" 的概率, 求数列 $\left\{p_n\right\}$ 的通项公式:
(3) 设事件 $X$ 为第 $k$ 个顾客参与时获得最后一个 "特等奖", 要使 $X$ 发生概率最大, 求 $k$ 的值.
贝塞尔曲线是由法国数学家 Pierre Bézier 发明的, 它为计算机矢量图形学奠定了基础. 贝塞尔曲线的有趣之处在于它的 "皮筋效应", 即随着控制点有规律地移动, 曲线会像皮筋一样伸缩, 产生视觉上的冲击.
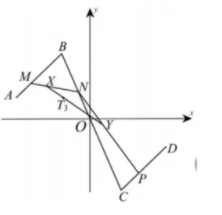
(1) 在平面直角坐标系中, 已知点 $T_1$ 在线段 $A B$ 上. 若 $A\left(x_1, y_1\right), B\left(x_2, y_2\right),\left|A T_1\right|=a|A B|$, 求动点 $T_1$坐标;
(2) 在平面直角坐标系中, 已知 $A(2,-4), B(-2,0), C(2,4)$, 点 $M, N$ 在线段 $A B, B C$ 上, 若动点 $T_2$在线段 $M N$ 上, 且满足 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{\left|M T_2\right|}{|M N|}=a$, 求动点 $T_2$ 的轨迹方程;
(3) 如图, 已知 $A\left(-\frac{\sqrt{6}}{3}, \frac{\sqrt{6}}{9}\right), B\left(-\frac{\sqrt{6}}{9}, \frac{\sqrt{6}}{3}\right), C\left(\frac{\sqrt{6}}{9},-\frac{\sqrt{6}}{3}\right), D\left(\frac{\sqrt{6}}{3},-\frac{\sqrt{6}}{9}\right)$, 若点 $M, N, P, X, Y, T_3$ 分别在线段 $A B, B C, C D, M N, N P, X Y$ 上, 且 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{|C P|}{|C D|}=\frac{|M X|}{|M N|}=\frac{|N Y|}{|N P|}=\frac{\left|X T_3\right|}{|X Y|}=a$, 求动点 $T_3$ 的轨迹方程.