贝塞尔曲线是由法国数学家 Pierre Bézier 发明的, 它为计算机矢量图形学奠定了基础. 贝塞尔曲线的有趣之处在于它的 "皮筋效应", 即随着控制点有规律地移动, 曲线会像皮筋一样伸缩, 产生视觉上的冲击.
(1) 在平面直角坐标系中, 已知点 $T_1$ 在线段 $A B$ 上. 若 $A\left(x_1, y_1\right), B\left(x_2, y_2\right),\left|A T_1\right|=a|A B|$, 求动点 $T_1$坐标;
(2) 在平面直角坐标系中, 已知 $A(2,-4), B(-2,0), C(2,4)$, 点 $M, N$ 在线段 $A B, B C$ 上, 若动点 $T_2$在线段 $M N$ 上, 且满足 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{\left|M T_2\right|}{|M N|}=a$, 求动点 $T_2$ 的轨迹方程;
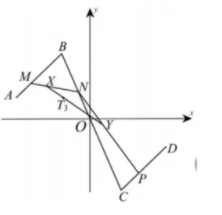
(3) 如图, 已知 $A\left(-\frac{\sqrt{6}}{3}, \frac{\sqrt{6}}{9}\right), B\left(-\frac{\sqrt{6}}{9}, \frac{\sqrt{6}}{3}\right), C\left(\frac{\sqrt{6}}{9},-\frac{\sqrt{6}}{3}\right), D\left(\frac{\sqrt{6}}{3},-\frac{\sqrt{6}}{9}\right)$, 若点 $M, N, P, X, Y, T_3$ 分别在线段 $A B, B C, C D, M N, N P, X Y$ 上, 且 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{|C P|}{|C D|}=\frac{|M X|}{|M N|}=\frac{|N Y|}{|N P|}=\frac{\left|X T_3\right|}{|X Y|}=a$, 求动点 $T_3$ 的轨迹方程.

(1) 在平面直角坐标系中, 已知点 $T_1$ 在线段 $A B$ 上. 若 $A\left(x_1, y_1\right), B\left(x_2, y_2\right),\left|A T_1\right|=a|A B|$, 求动点 $T_1$坐标;
(2) 在平面直角坐标系中, 已知 $A(2,-4), B(-2,0), C(2,4)$, 点 $M, N$ 在线段 $A B, B C$ 上, 若动点 $T_2$在线段 $M N$ 上, 且满足 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{\left|M T_2\right|}{|M N|}=a$, 求动点 $T_2$ 的轨迹方程;
(3) 如图, 已知 $A\left(-\frac{\sqrt{6}}{3}, \frac{\sqrt{6}}{9}\right), B\left(-\frac{\sqrt{6}}{9}, \frac{\sqrt{6}}{3}\right), C\left(\frac{\sqrt{6}}{9},-\frac{\sqrt{6}}{3}\right), D\left(\frac{\sqrt{6}}{3},-\frac{\sqrt{6}}{9}\right)$, 若点 $M, N, P, X, Y, T_3$ 分别在线段 $A B, B C, C D, M N, N P, X Y$ 上, 且 $\frac{|A M|}{|A B|}=\frac{|B N|}{|B C|}=\frac{|C P|}{|C D|}=\frac{|M X|}{|M N|}=\frac{|N Y|}{|N P|}=\frac{\left|X T_3\right|}{|X Y|}=a$, 求动点 $T_3$ 的轨迹方程.