单选题 (共 8 题 ),每题只有一个选项正确
下列命题是真命题的是
$\text{A.}$ 两个四棱锥可以拼成一个四棱柱
$\text{B.}$ 正三棱锥的底面和侧面都是等边三角形
$\text{C.}$ 经过不共线的三个点的球有且只有一个
$\text{D.}$ 直棱柱的侧面是矩形
已知全集 $U=\mathrm{R}$, 集合 $A=$ $\left\{x \mid x-2 x^2 \geq-15\right\}, B=\{x \mid x \leq-3$ 或 $x \geq 2\}$, 则 $A \cap C_U B=$
$\text{A.}$ $\left.-\frac{5}{2}, 2\right)$
$\text{B.}$ $-3,-\frac{5}{2}$
$\text{C.}$ $(-3,3]$
$\text{D.}$ $(2,3]$
已知 $z$ 是虚数, $z^2+2 z$ 是实数, 则 $z$的
$\text{A.}$ 实部为 1
$\text{B.}$ 实部为 -1
$\text{C.}$ 虚部为 1
$\text{D.}$ 虚部为 -1
已知数列 $\left\{3^{a_n}\right\}$ 是公比为 $3^{a_1}$ 的等比数列, $S_n$ 是数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 则 $\frac{S_5}{a_5}=(\quad)$
$\text{A.}$ 1
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ 3
在 $\triangle A B C$ 中, 已知 $a=a \cos B+b \cos A=1, \sin C=\frac{\sqrt{2}}{2}$, 则
$\text{A.}$ $b=1$
$\text{B.}$ $b=\sqrt{2}$
$\text{C.}$ $c=\sqrt{2}$
$\text{D.}$ $c=\sqrt{3}$
质监部门对某种建筑构件的抗压能力进行检测,对此建筑构件实施两次打击,若没有受损,则认为该构件通过质检.若第一次打击后该构件没有受损的概率为 0.85 ,当第一次没有受损时第二次实施打击也没有受损的概率为 0.80 ,则该构件通过质检的概率为
$\text{A.}$ 0.4
$\text{B.}$ 0.16
$\text{C.}$ 0.68
$\text{D.}$ 0.17
已知平行六面体 $A B C D-A_1 B_1 C_1 D_1$中, $A A_1=2, B D=3, \overrightarrow{A D_1} \cdot \overrightarrow{D C}-\overrightarrow{A B_1} \cdot \overrightarrow{B C}=4$, 则 $\cos \left\langle\overrightarrow{A A_1}, \overrightarrow{B D}\right\rangle=(\quad)$
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $-\frac{2}{3}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $-\frac{3}{4}$
若存在直线与曲线 $f(x)=x^3-x, g(x)=x^2+a$ 都相切,则 $a$ 的范围为
$\text{A.}$ $[-1,+\infty)$
$\text{B.}$ $\left[-1, \frac{5}{27}\right]$
$\text{C.}$ $\left[\frac{5}{27},+\infty\right)$
$\text{D.}$ $\left[-\infty, \frac{5}{27}\right]$
多选题 (共 3 题 ),每题有多个选项正确
甲乙两名同学参加系列知识问答节目,甲同学参加了 5 场,得分是 $3,4,5,5,8$ ,乙同学参加了 7 场,得分是 $3,3,4$ , $5 , 5 , 7 , 8$ ,那么有关这两名同学得分数据下列说法正确的是
$\text{A.}$ 得分的中位数甲比乙要小
$\text{B.}$ 两人的平均数相同
$\text{C.}$ 两人得分的极差相同
$\text{D.}$ 得分的方差甲比乙小
已知圆 $C_1: x^2+y^2=1$, 圆 $C_2:(x-$ $3)^2+(y+4)^2=r^2(r>0), P 、 Q$ 分别是圆 $C_1$ 与圆 $C_2$ 上的点, 则
$\text{A.}$ 若圆 $C_1$ 与圆 $C_2$ 无公共点, 则 $0 < r < 4$
$\text{B.}$ 当 $\mathrm{r}=5$ 时, 两圆公共弦所在直线方程为 $6 x-8 y-1=0$
$\text{C.}$ 当 $r=2$ 时,则 $P Q$ 斜率的最大值为 $-\frac{7}{24}$
$\text{D.}$ 当 $r=3$ 时, 过 $P$ 点作圆 $C_2$ 两条切线, 切点分别为 $A, B$, 则 $\angle A P B$ 不可能等于 $\frac{\pi}{2}$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, f(x+y)+2 x y=f(x)+f(y), f(1)=2$ ,则
$\text{A.}$ $f(0)=0$
$\text{B.}$ $f(-2)=-10$
$\text{C.}$ $y=f(x)+x^2$ 是奇函数
$\text{D.}$ $y=f(x)-x^2$ 是偶函数
填空题 (共 3 题 ),请把答案直接填写在答题纸上
$(x-2 y+1)^5$ 展开式中含 $x^2 y$ 项的系数为
圆台的上、下底面及侧面都相切的球, 称为圆台的内切球, 若圆台的上下底面半径为 $r_1, r_2$, 且 $r_1 \cdot r_2=1$, 则它的内切球的体积为
|椭圆 $C: \frac{y^2}{a^2}+\frac{x^2}{b^2}=1(a>b>0)$ 的左、右顶点分别为 $A, B$, 点 $P$ 在椭圆上第一象限内, 记 $\angle P A B=\alpha, \angle P B A=\beta$, 存在圆 $N$ 经过点 $P, A, B$, 且 $\overrightarrow{N A} \cdot \overrightarrow{N B}=0, \tan ^\alpha+{ }_{\tan } \beta=8$, 则椭圆 $C$的离心率为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
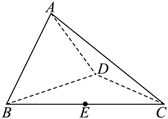
如图,四面体 $A B C D$ 中, $E$ 是 $B C$ 的中点, $C A=C B=C D=B D=2, A B=A D=\sqrt{2}$
(1) 求异面直线 $A B$ 与 $C D$ 所成角余弦值的大小;
(2) 求点 $E$ 到平面 $A C D$ 的距离.
已知函数 $f(x)=\ln x-a x, g(x)=$ $\frac{2}{a x}, a \neq 0$.
(1) 求函数 $f(x)$ 的单调区间;
(2) 若 $f(x) \leq g(x)$ 恒成立, 求 $a$ 的最小值.
11 分制乒乓球比赛规则如下: 在一局比赛中, 每两球交换发球权, 每赢一球得 1 分, 先得 11 分且至少领先 2 分者胜, 该局比赛结束:当某局比分打成 $10: 10$ 后, 每球交换发球权,领先 2 分者胜,该局比赛结束现有甲、乙两人进行一场五局三胜、每局 11 分制的乒乓球比赛,比赛开始前通过抛掷一枚质地均匀的硬币来确定谁先发球假设甲发球时甲得分的概率为 $\frac{2}{3}$, 乙发球时甲得分的概率为 $\frac{1}{2}$, 各球的比赛结果相互独立, 且各局的比赛结果也相互独立.
(1)若每局比赛甲获胜的概率 $p=\frac{2}{3}$, 求该场比赛甲获胜的概率.
(2)已知第一局目前比分为 $10: 10$, 求
(i) 再打两个球甲新增的得分 $X$ 的分布列和均值;
(ii) 第一局比赛甲获胜的概率 $p_0$;
如图, 小明同学先把一根直尺固定在画板上面, 把一块三角板的一条直角边紧靠在直尺边沿, 再取一根细绳, 它的长度与另一直角边相等, 让细绳的一端固定在三角板的顶点 $A$处, 另一端固定在画板上点 $F$ 处, 用铅笔尖扣紧绳子 (使两段细绳绷直), 靠住三角板,然后将三角板沿着直尺上下滑动, 这时笔尖在平面上画出了圆锥曲线 $C$ 的一部分图象. 已知细绳长度为 3 , 经测量, 当笔尖运动到点 $P$ 处, 此时, $\angle F A P=30^{\circ}, \angle A F P=90^{\circ}$. 设直尺边沿所在直线为 $a$, 以过 $F$ 垂直于直尺的直线为 $x$ 轴, 以过 $F$ 垂直于 $a$ 的垂线段的中垂线为 $y$ 轴, 建立平面直角坐标系.
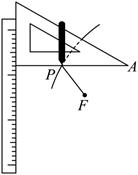
(1) 求曲线 $C$ 的方程;
(2)斜率为 $k$ 的直线 $l$ 过点 $D(0,-3)$, 且与曲线 $C$ 交于不同的两点 $M, N$, 已知 $k$ 的取值范围为 $(0,2)$, 若 $\overrightarrow{D M}=\lambda \overrightarrow{D N}$, 求 $\lambda$ 的范围.
数学家发现: $\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$,其中 $n!=1 \times 2 \times 3 \times \cdots \times n$. 利用该公式可以得到: 当 $x$ $\in\left(0, \frac{\pi}{2}\right)$ 时, $\sin x < x ; \sin x>x-\frac{x^3}{3!} ; \sin x < x-\frac{x^3}{3}+\frac{x^5}{5!} ; \cdots$.
(1) 证明: 当 $x \in\left(0, \frac{\pi}{2}\right)$ 时, $\frac{\sin x}{x}>\frac{1}{2}$;
(2) 设 $f(x)=m \sin x$, 当 $f(x)$ 的定义域为 $[a, b]$ 时,值域也为 $[a, b]$,则称 $[a, b]$ 为 $f(x)$ 的"和谐区间". 当 $m$ $=-2$ 时, $f(x)$ 是否存在 "和谐区间" ? 若存在,求出 $f(x)$ 的所有 "和谐区间", 若不存在,请说明理由.