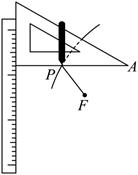
如图, 小明同学先把一根直尺固定在画板上面, 把一块三角板的一条直角边紧靠在直尺边沿, 再取一根细绳, 它的长度与另一直角边相等, 让细绳的一端固定在三角板的顶点 $A$处, 另一端固定在画板上点 $F$ 处, 用铅笔尖扣紧绳子 (使两段细绳绷直), 靠住三角板,然后将三角板沿着直尺上下滑动, 这时笔尖在平面上画出了圆锥曲线 $C$ 的一部分图象. 已知细绳长度为 3 , 经测量, 当笔尖运动到点 $P$ 处, 此时, $\angle F A P=30^{\circ}, \angle A F P=90^{\circ}$. 设直尺边沿所在直线为 $a$, 以过 $F$ 垂直于直尺的直线为 $x$ 轴, 以过 $F$ 垂直于 $a$ 的垂线段的中垂线为 $y$ 轴, 建立平面直角坐标系.
(1) 求曲线 $C$ 的方程;
(2)斜率为 $k$ 的直线 $l$ 过点 $D(0,-3)$, 且与曲线 $C$ 交于不同的两点 $M, N$, 已知 $k$ 的取值范围为 $(0,2)$, 若 $\overrightarrow{D M}=\lambda \overrightarrow{D N}$, 求 $\lambda$ 的范围.

(1) 求曲线 $C$ 的方程;
(2)斜率为 $k$ 的直线 $l$ 过点 $D(0,-3)$, 且与曲线 $C$ 交于不同的两点 $M, N$, 已知 $k$ 的取值范围为 $(0,2)$, 若 $\overrightarrow{D M}=\lambda \overrightarrow{D N}$, 求 $\lambda$ 的范围.