单选题 (共 11 题 ),每题只有一个选项正确
“ $a>\frac{1}{2}$ ” 是 “ $\frac{1}{a} < 2$ ” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 既不充分也不必要条件
$\text{D.}$ 充要条件
在 3 与 15 之间插入 3 个数, 使这 5 个数成等差数列, 则插入的 3 个数之和为
$\text{A.}$ 21
$\text{B.}$ 24
$\text{C.}$ 27
$\text{D.}$ 30
已知 $\triangle A B C$ 的内角 $A 、 B 、 C$ 的对边分别为、 $b 、 c$, 若 $A=60^{\circ}, b=10$, 则下列 $a$ 的取值中, 使得该三角形有两解的是
$\text{A.}$ $a=8$
$\text{B.}$ $a=9$
$\text{C.}$ $a=10$
$\text{D.}$ $a=11$
$\left(1+\frac{1}{x^3}\right)(1+x)^7$ 展开式中 $x^3$ 项的系数为
$\text{A.}$ 42
$\text{B.}$ 35
$\text{C.}$ 7
$\text{D.}$ 1
已知函数 $f(x)=\ln \frac{m+x}{1-n-x}(m>0, n>0)$ 是奇函数, 则 $\frac{1}{m}+\frac{2}{n}$ 的最小值为
$\text{A.}$ 3
$\text{B.}$ 5
$\text{C.}$ $3+2 \sqrt{2}$
$\text{D.}$ $3+4 \sqrt{2}$
在复数范围内, 下列命题是真命题的为
$\text{A.}$ 若 $z \neq 0$, 则 $z-\bar{z}$ 是纯虚数
$\text{B.}$ 若 $z^2=-|z|^2$, 则 $z$ 是纯虚数
$\text{C.}$ 若 $z_1^2+z_2^2=0$, 则 $z_1=0$ 且 $z_2=0$
$\text{D.}$ 若 $z_1, z_2$ 为虚数, 则 $z_1 \bar{z}_2+\bar{z}_1 z_2 \in \mathrm{R}$
已知圆锥的顶点为 $S, O$ 为底面圆心, 母线 $S A$ 与 $S B$ 互相垂直, $\square S A B$ 的面积为 $8, S A$ 与圆锥底面所成的角为 $30^{\circ}$, 则
$\text{A.}$ 圆锥的高为 1
$\text{B.}$ 圆锥的体积为 $24 \pi$
$\text{C.}$ 圆椎侧面展开图的圆心角为 $\frac{2 \sqrt{3} \pi}{3}$
$\text{D.}$ 二面角 $S-A B-O$ 的大小为 $45^{\circ}$
如图, 设 $F_1, F_2$ 是椭圆的左、右焦点, 点 $P$ 是以 $F_1 F_2$ 为直径的圆与椭圆在第一象限内的交点, 延长 $P F_2$ 与椭圆交于点 $Q$, 若 $\left|P F_1\right|=4\left|Q F_2\right|$, 则直线 $P F_2$ 的斜率为
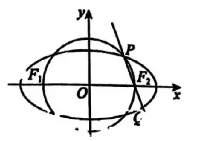
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ -1
$\text{C.}$ -2
$\text{D.}$ -3
某次数学考试后, 为分析学生的学习情况, 某校从某年级中随机抽取了 100 名学生的成绩, 整理得到如图所示的频率分布直方图.为进一步分析高分学生的成绩分布情况, 计算得到这 100 名学生中, 成绩位于 $[80,90)$ 内的学生成绩方差为 12 , 成绩位于 $[90,100)$ 内的同学成绩方差为 10 . 则
参考公式: 样本划分为 2 层, 各层的容量、平均数和方差分别为: $m, \bar{x}, s_1^2 ; n, \bar{y}, s_2^2$. 记样本平均数为 $\bar{\omega}$, 样本方差为 $s^2, s^2=\frac{m}{m+n}\left[s_1^2+(\bar{x}-\bar{\omega})^2\right]+\frac{n}{m+n}\left[s_2^2+(\bar{y}-\bar{\omega})^2\right]$
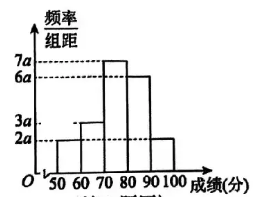
$\text{A.}$ $a=0.004$
$\text{B.}$ 估计该年级学生成绩的中位数为 77.14
$\text{C.}$ 估计该年级成绩在 80 分及以上的学生成绩的平均数为 87.50
$\text{D.}$ 估计该年级成绩在 80 分及以上的学生成绩的方差为 30.25
已知函数 $f(x)=\cos 2 x \cdot \cos \left(2 x+\frac{\pi}{6}\right)-\frac{\sqrt{3}}{4}$, 则()
$\text{A.}$ 曲线 $y=f(x)$ 的对称轴为 $x=k \pi-\frac{\pi}{6}, k \in \mathrm{Z}$
$\text{B.}$ $f(x)$ 在区间 $\left(\frac{\pi}{4}, \frac{\pi}{3}\right)$ 上单调递増
$\text{C.}$ $f(x)$ 的最大值为 $\frac{1}{2}$
$\text{D.}$ $f(x)$ 在区间 $[0,2 \pi]$ 上的所有零点之和为 $8 \pi$
如图, $O A$ 是连接河岸 $A B$ 与 $O C$ 的一座古桥, 因保护古迹与发展的需要, 现规划建一座新桥 $B C$, 同时设立一个圆形保护区. 规划要求:
①新桥 $B C$ 与河岸 $A B$ 垂直;
②保护区的边界为一个圆, 该圆与 $B C$ 相切,且圆心 $M$ 在线段 $O A$ 上;
③古桥两端 $O$ 和 $A$ 到该圆上任意一点的距离均不少于 $80 \mathrm{~m}$.
经测量, 点 $A 、 C$ 分别位于点 $O$ 正北方向 $60 \mathrm{~m}$ 、正东方向 $170 \mathrm{~m}$ 处, $\tan \angle B C O=\frac{4}{3}$, 根据图中所给的平面直.角坐标系, 下列结论中, 正确的是
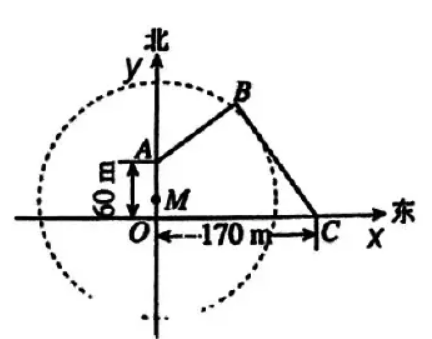
$\text{A.}$ 新桥 $B C$ 的长为 $150 \mathrm{~m}$
$\text{B.}$ 圆心 $M$ 可以在点 $A$ 处
$\text{C.}$ 圆心 $M$ 到点 $O$ 的距离至多为 $35 \mathrm{~m}$
$\text{D.}$ 当 $O M$ 长为 $20 \mathrm{~m}$ 时, 圆形保护区的面积最大
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知成对样本数据 $\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_n, y_n\right)(n \geq 2)$ 中, $x_1, x_2, \cdots, x_n$ 不全相等, 且所有样本点 $\left(x_i, y_i\right)(i=1,2, \cdots, n)$ 都在直线 $y=\frac{1}{2} x+1$ 上, 则这组成对样本数据的样本相关系数 $r=$
已知 $\triangle A B C$ 外接圆的半径为 1 , 圆心为点 $O$, 且满足 $4 \overrightarrow{O C}=-2 \overrightarrow{O A}-3 \overrightarrow{O B}$, 则 $\cos \angle A O B=$
如图, 在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $E$ 是棱 $C C_1$ 的中点, 记平面 $A D_1 E$ 与平面 $A B C D$ 的交线为 $l_1$, 平面 $A D_1 E$ 与平面 $A B B_1 A_1$ 的交线为 $l_2$, 若直线 $A B$ 分别与 $l_1 l_2$ 所成的角为 $\alpha, \beta$, 则 $\tan \alpha=$ $\qquad$ $\tan (\alpha+\beta)=$
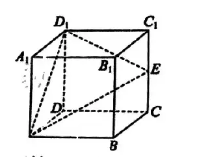
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{a_n\right\}$ 和 $\left\{b_n\right\}$, 其中 $b_n=2^{a_n}, n \in \mathrm{N}^*$, 数列 $\left\{a_n+b_n\right\}$ 的前 $n$ 项和为 $S_n$.
(1) 若 $a_n=2 n$, 求 $S_n$;
(2) 若 $\left\{b_n\right\}$ 是等比数列, $S_n=3 n$, 求数列 $\left\{a_n\right\}$ 和 $\left\{b_n\right\}$ 的通项公式.
已知函数 $f(x)=a x-\frac{1}{x}-(a+1) \ln x(a \in \mathrm{R})$.
(1) 当 $a=-1$ 时, 求曲线 $y=f(x)$ 在点 $(\mathrm{e}, f(\mathrm{e}))$ 处的切线方程;
(2) 若 $f(x)$ 既存在极大值, 又存在极小值, 求实数 $a$ 的取值范围.
如图, 三棱台 $A B C-A_1 B_1 C_1$ 中, 侧面四边形 $A C C_1 A_1$ 为等腰梯形, 底面三角形 $A B C$ 为正三角形, 且 $A C=2 A_1 C_1=2$. 设 $D$ 为棱 $A_1 C_1$ 上的点.
(1) 若 $D$ 为 $A_1 C_1$ 的中点, 求证: $A C \perp B D$;
(2) 若三棱台 $A B C-A_1 B_1 C_1$ 的体积为 $\frac{7}{8}$, 且侧面 $A C C_1 A_1 \perp$ 底面 $A B C$, 试探究是否存在点 $D$, 使直线 $B D$ 与平面 $B C C_1 B_1$ 所成角的正弦值为 $\frac{\sqrt{15}}{10}$ ? 若存在, 确定点 $D$ 的位置;若不存在, 说明理由.
已知点 $M\left(x_0, y_0\right)$ 为双曲线 $\frac{x^2}{2}-y^2=1$ 上的动点.
(1) 判断直线 $\frac{x_0 x}{2}-y_0 y=1$ 与双曲线的公共点个数, 并说明理由;
(2) (i)如果把 (1) 的结论推广到一般双曲线, 你能得到什么相应的结论? 请写出你的结论, 不必证明;
(ii) 将双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的两条渐近线称为“退化的双曲线”, 其方程为 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=0$, 请利用该方程证明如下命题: 若 $T(m, n)$ 为双曲线 $C$ 上一点, 直线 $l: \frac{m x}{a^2}-\frac{n y}{b^2}=1$ 与 $C$ 的两条浙近线分别交于点 $P 、 Q$, 则 $T$ 为线段 $P Q$ 的中点.
2023年11月,我国教育部发布了《中小学实验教学基本目录》, 内容包括高中数学在内共有 16 个学科 900 多项实验与实践活动.我市某学校的数学老师组织学生到“牛田洋”进行科学实践活动,在某种植番石榴的果园中,老师建议学生尝试去摘全园最大的番石榴,规定只能摘一次,并且只可以向前走,不能回头.结果,学生小明两手空空走出果园, 因为他不知道前面是否有更大的, 所以没有摘, 走到前面时,又发觉总不及之前见到的,最后什么也没摘到.
假设小明在果园中一共会遇到 $n$ 颗番石榴(不妨设 $n$ 颗番石榴的大小各不相同), 最大的那颗番石榴出现在各个位置上的概率相等, 为了尽可能在这些番石榴中摘到那颗最大的,小明在老师的指导下采用了如下策略:不摘前 $k(1 \leq k < n)$ 颗番石榴,自第 $k+1$ 颗开始,只要发现比他前面见过的番石榴大的,就摘这颗番石榴,否则就摘最后一颗.设 $k=t n$, 记该学生摘到那颗最大番不榴的概率为 $P$.
(1) 若 $n=4, k=2$, 求 $P$;
(2)当 $n$ 趋向于无穷大时,从理论的角度,求 $P$的最大值及 $P$ 取最大值时 $t$ 的值.
$$
\text { (取 } \frac{1}{k}+\frac{1}{k+1}+\cdots+\frac{1}{n-1}=\ln \frac{n}{k} \text { ) }
$$