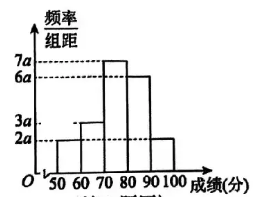
某次数学考试后, 为分析学生的学习情况, 某校从某年级中随机抽取了 100 名学生的成绩, 整理得到如图所示的频率分布直方图.为进一步分析高分学生的成绩分布情况, 计算得到这 100 名学生中, 成绩位于 $[80,90)$ 内的学生成绩方差为 12 , 成绩位于 $[90,100)$ 内的同学成绩方差为 10 . 则
参考公式: 样本划分为 2 层, 各层的容量、平均数和方差分别为: $m, \bar{x}, s_1^2 ; n, \bar{y}, s_2^2$. 记样本平均数为 $\bar{\omega}$, 样本方差为 $s^2, s^2=\frac{m}{m+n}\left[s_1^2+(\bar{x}-\bar{\omega})^2\right]+\frac{n}{m+n}\left[s_2^2+(\bar{y}-\bar{\omega})^2\right]$