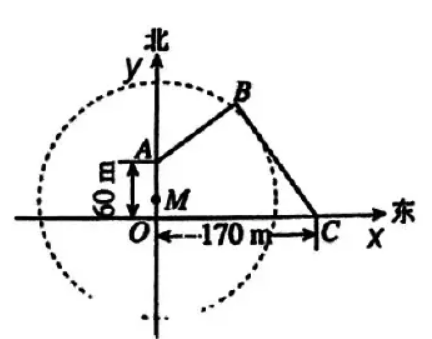
如图, $O A$ 是连接河岸 $A B$ 与 $O C$ 的一座古桥, 因保护古迹与发展的需要, 现规划建一座新桥 $B C$, 同时设立一个圆形保护区. 规划要求:
①新桥 $B C$ 与河岸 $A B$ 垂直;
②保护区的边界为一个圆, 该圆与 $B C$ 相切，且圆心 $M$ 在线段 $O A$ 上;
③古桥两端 $O$ 和 $A$ 到该圆上任意一点的距离均不少于 $80 \mathrm{~m}$.
经测量, 点 $A 、 C$ 分别位于点 $O$ 正北方向 $60 \mathrm{~m}$ 、正东方向 $170 \mathrm{~m}$ 处, $\tan \angle B C O=\frac{4}{3}$, 根据图中所给的平面直.角坐标系, 下列结论中, 正确的是
$\text{A.}$ 新桥 $B C$ 的长为 $150 \mathrm{~m}$
$\text{B.}$ 圆心 $M$ 可以在点 $A$ 处
$\text{C.}$ 圆心 $M$ 到点 $O$ 的距离至多为 $35 \mathrm{~m}$
$\text{D.}$ 当 $O M$ 长为 $20 \mathrm{~m}$ 时, 圆形保护区的面积最大