单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{x \mid-1 < x \leqslant 2\}, B=\{-1,0,1,2\}$, 则 $A \cap B=$
$\text{A.}$ $\{-1,0,1\}$
$\text{B.}$ $\{-1,0\}$
$\text{C.}$ $\{0,1\}$
$\text{D.}$ $\{0,1,2\}$
已知 $(1-a \mathrm{i})(2+\mathrm{i})=b+3 \mathrm{i}$ ( $\mathrm{i}$ 为虚数单位), 其中 $a, b$ 为实数, 则 $a, b$ 的值 分别为
$\text{A.}$ $-1,1$
$\text{B.}$ $1,-1$
$\text{C.}$ $1,1$
$\text{D.}$ $-1,-1$
设 $P$ 是双曲线 $\frac{x^2}{16}-\frac{y^2}{20}=1$ 上一点, $F_1, F_2$ 分别是双曲线左、右两个焦 点, 若 $\left|P F_1\right|=9$, 则 $\left|P F_2\right|$ 等于
$\text{A.}$ 1
$\text{B.}$ 8
$\text{C.}$ 17
$\text{D.}$ 1 或 17
为了庆祝中国共产党第二十次全国代表大会, 学校采用按比例分配的分 层随机抽样的方法从高一 1002 人, 高二 1002 人, 高三 1503 人中抽取 126 人观看 “中国共产党第二十次全国代表大会”直播, 那么高三年级被 抽取的人数为
$\text{A.}$ 36
$\text{B.}$ 42
$\text{C.}$ 50
$\text{D.}$ 54
一个圆锥的侧面展开图是圆心角为 $\frac{2 \pi}{3}$, 弧长为 $2 \pi$ 的扇形, 则该圆雉 轴截面的面积 $S=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $2 \sqrt{2}$
$\text{D.}$ $2 \sqrt{5}$
已知 $\cos \left(\frac{\pi}{4}-\alpha\right)=\frac{3}{5}, \sin \left(\frac{5 \pi}{4}+\beta\right)=-\frac{12}{13}, \alpha \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right), \beta \in\left(0, \frac{\pi}{4}\right)$, 则 $\sin (\alpha+\beta)$ 的值为
$\text{A.}$ $\frac{56}{65}$
$\text{B.}$ $\frac{33}{65}$
$\text{C.}$ $-\frac{16}{65}$
$\text{D.}$ $-\frac{63}{65}$
某学生进行投篮训练, 采取积分制, 有 7 次投篮机会, 投中一次得 1 分, 不 中得 0 分, 若连续投中两次则额外加 1 分, 连续投中三次额外加 2 分, 以此 类推, 连续投中七次额外加 6 分, 假设该学生每次投中的概率是 $\frac{1}{2}$, 且每次 投中之间相互独立, 则该学生在此次训练中恰好得 7 分的概率是
$\text{A.}$ $\frac{9}{128}$
$\text{B.}$ $\frac{5}{64}$
$\text{C.}$ $\frac{11}{128}$
$\text{D.}$ $\frac{3}{32}$
设 $a=\frac{2}{21}, b=\sin \frac{2}{21}, c=\ln \frac{11}{10}$, 则
$\text{A.}$ $a>b>c$
$\text{B.}$ $a>c>b$
$\text{C.}$ $c>a>b$
$\text{D.}$ $b>c>a$
多选题 (共 4 题 ),每题有多个选项正确
已知 $m, n$ 是两条不重合的直线, $\alpha, \beta$ 是两个不重合的平面, 下列命题 不正确的是
$\text{A.}$ 若 $m / / \alpha, m / / \beta, n / / \alpha, n / / \beta$, 则 $\alpha / / \beta$
$\text{B.}$ 若 $m \perp n, m / / \alpha, n \perp \beta$, 则 $\alpha \perp \beta$
$\text{C.}$ 若 $m \perp n, m \subset \alpha, n \subset \beta$, 则 $\alpha \perp \beta$
$\text{D.}$ 若 $m / / n, m \perp \alpha, n \perp \beta$, 则 $\alpha / / \beta$
已知圆 $M: x^2+y^2+2 x-4 y+1=0$, 以下结论正确的是
$\text{A.}$ 过点 $A(1,2)$ 与圆 $M$ 相切的直线方程为 $x=1$
$\text{B.}$ 圆 $M$ 与圆 $N:(x+4)^2+(y-6)^2=1$ 相交
$\text{C.}$ 过点 $(1,1)$ 可以作两条直线与圆 $M$ 相切
$\text{D.}$ 圆 $M$ 上的点到直线 $4 x-3 y+5=0$ 的距离的最大值为 3
在平面直角坐标系 $x O y$ 中, 点 $F$ 是抛物线 $C: y^2=a x(a>0)$ 的焦点, 两 点 $A\left(\frac{a}{16}, 1\right), B(a, b)(b < 0)$ 在抛物线 $C$ 上, 则下列说法正确的是
$\text{A.}$ 抛物线 $C$ 的方程为 $y^2=4 x$
$\text{B.}$ $b=-4$
$\text{C.}$ 以 $A B$ 为直径的圆的方程是 $\left(x-\frac{17}{8}\right)^2+\left(y+\frac{3}{2}\right)^2=\frac{25}{8}$
$\text{D.}$ $A, F, B$ 三点共线
定义在 $\mathbf{R}$ 上的函数 $f(x)$ 的导函数为 $f^{\prime}(x)$, 且 $3 f(x)+x f^{\prime}(x)>0$, 则 对任意 $x_1 < x_2$, 下列结论成立的是
$\text{A.}$ $\frac{x_1^3}{x_2^3} < \frac{f\left(x_2\right)}{f\left(x_1\right)}$
$\text{B.}$ $\mathrm{e}^{3 x_1} f\left(\mathrm{e}^{x_1}\right)>0$
$\text{C.}$ 不存在 $x_1, x_2$, 使得 $x_1^6 f\left(x_1^2\right)=x_2^6 f\left(x_2^2\right)$
$\text{D.}$ 存在 $x_1, x_2$, 使得 $\frac{x_1^3}{x_2^3} f\left(\frac{x_1}{x_2}\right) < f(1)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $|\boldsymbol{a}|=3, \boldsymbol{b}=(1,2)$, 则 $(\boldsymbol{a}+\boldsymbol{b}) \cdot(\boldsymbol{a}-\boldsymbol{b})=$
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 已知 $a_1+a_3+a_7+a_9=28$, 则 $S_9=$
已知函数 $f(x)=1-\sin \left(\frac{\pi}{3} x+\frac{\pi}{6}\right)$, 则 $f(1)+f(2)+f(3)+\cdots+$ $f(2023)=$
当 $x \in[-2,1]$ 时, 不等式 $a x^3-x^2+4 x+3 \geqslant 0$ 恒成立, 则实数 $a$ 的 取值范围是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $a, b, c$ 分别为 $\triangle A B C$ 内角 $A, B, C$ 的对边, 且 $c \sin B \sin C$ $=(c \cos B+2 b-a) \cos \mathrm{C}$.
(1) 求角 $C$;
(2) 若 $c^2=2 a b, \triangle A B C$ 的面积为 $\sqrt{3}$, 求 $a+b$ 的值.
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, S_3=620, S_{n+1}=5 S_n+20$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 若 $b_n=\log _5 \frac{a_n}{4}$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 求 $\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T_3}+\cdots$
$$
+\frac{1}{T_n} .
$$
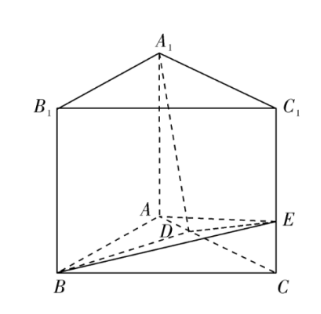
如图所示, 直三棱柱 $A B C-A_1 B_1 C_1$ 中, $A B \perp A C, A B=A C=$ $A A_1=3, A D=\frac{1}{3} A C, C E=\frac{1}{3} C C_1$.
(1) 求证: $A_1 D \perp B E$;
(2) 求直线 $A_1 D$ 与平面 $B D E$ 所成角的正弦值.
元宵佳节, 是民间最重要的民俗节日之一. 在某庆祝活动现 场, 为了解观众对该活动的观感情况 (“一般”或“激动”), 现从该活动 现场的观众中随机抽取 200 名, 得到下表:

(1)填补上面的 $2 \times 2$ 列联表, 并依据小概率值 $\alpha=0.1$ 的独立性检 验, 能否认为性别与对该活动的观感程度有关?
(2)该活动现场还举行了有奖促销活动, 凡当天消费每满 300 元, 可 抽奖一次. 抽奖方案是: 从装有 3 个红球和 3 个白球 (形状、大小、 质地完全相同) 的抽奖箱里一次性摸出 2 个球, 若摸出 2 个红球, 则可获得 100 元现金的返现; 若摸出 1 个红球,则可获得 50 元现 金的返现; 若没摸出红球, 则不能获得任何现金返现. 若某观众当 天消费 600 元, 记该观众参加抽奖获得的返现金额为 $X$, 求随机 变量 $X$ 的分布列和数学期望.
附 : $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$, 其中 $n=a+b+c+d$.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 点 $B$ 是椭圆 $C$ 的上顶点, $\triangle B F_1 F_2$ 是等边三角形, $\triangle B F_1 F_2$ 的内切圆 的面积为 $\frac{\pi}{3}$.
(1) 求椭圆 $C$ 的方程;
(2) 已知 $T$ 在 $x$ 轴负半轴上且 $|O T|=4\left|O F_1\right|$, 过 $T$ 的直线与椭圆交于 $M, N$ 两点, 求 $\triangle M N F_1$ 面积的最大值.
已知函数 $f(x)=\mathrm{e}^{\mathrm{e}^{x-t}-t}$.
(1) 若 $f(x)$ 在 $(t, f(t))$ 处的切线方程平行于直线 $x-y+1=0$, 求 $t$ 的 值以及此时的切线方程;
(2) 若方程 $f(x)=x$ 在 $(0,+\infty)$ 上有两个不同的实数根, 求实数 $t$ 的取 值范围.