解答题 (共 20 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲、乙两人组成"星队"参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为 $\frac{2}{3}$ ,乙每轮猜对的概率为 $p$ 。在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响。已知"星队"在第一轮活动中猜对 1 个成语的概率为 $\frac{1}{2}$ .
(1)求 $p$ 的值;
(2)记"星队"在两轮活动中猜对成语的总数为 $X$ ,求 $X$ 的分布列与期望.
中国共产党第二十次全国代表大会于 2022 年 10 月 16 日至 22 日在北京人民大会堂顺利召开。某部门组织相关单位采取多种形式学习宣传和贯彻党的二十大精神。其中"学习二十大"进行竞赛。甲、乙两单位在联合开展主题学习及知识竞赛活动中通过此栏目进行比赛,比赛规则是:每一轮比赛中每个单位派出一人代表其所在单位答题,两单位都全部答对或者都没有全部答对则均记 0 分;一单位全部答对而另一单位没有全部答对,则全部答对的单位记 1 分,没有全部答对的单位记 -1 分,设每轮比赛中甲单位全部答对的概率为 $\frac{2}{3}$ ,乙单位全部答对的概率为 $\frac{3}{5}$ ,甲、乙两单位答题相互独立,且每轮比赛互不影响。
(1)经过 1 轮比赛,设甲单位的记分为 $X$ ,求 $X$ 的分布列和期望;
(2)若比赛采取 3 轮制,试计算第 3 轮比赛后甲单位累计得分低于乙单位累计得分的概率.
某学校最近考试频繁,为了减轻同学们的学习压力,班上决定进行一次减压游戏.班主任把 8 个小球(只是颜色不同)放入一个袋子里,其中白色球与黄色球各 3个,红色球与绿色球各 1 个.现甲、乙两位同学进行摸球得分比赛,摸到白球每个记 1 分,黄球每个记 2 分,红球每个记 3 分,绿球每个记 4 分,规定摸球人得分不低于 8 分为获胜,否则为负.并规定如下:
① 一个人摸球,另一人不摸球;
② 摸球的人摸出的球后不放回;
③ 摸球的人先从袋子中摸出 1 球;若摸出的是绿色球,则再从袋子里摸出 2 个球;若摸出的不是绿色球,则再从袋子里摸出 3 个球,摸球人的得分为两次摸出的球的记分之和。
(1)若由甲摸球,如果甲先摸出了绿色球,求该局甲获胜的概率;
(2)若由乙摸球,如果乙先摸出了红色球,求该局乙得分 $\xi$ 的分布列和数学期望 $E(\xi)$ ;
某学校组织"消防"知识竞赛,有 $A, B$ 两类题目.每位参加比赛的同学先在两类题目中选择一类并从中随机抽取一道题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.$A$ 类问题中的每个问题回答正确得 40 分,否则得 0 分;$B$ 类问题中的每个问题回答正确得 60 分,否则得 0 分已知小明能正确回答 $A$类问题的概率为 0.7 ,能正确回答 $B$ 类问题的概率为 0.5 ,且能正确回答问题的概率与回答次序无关
(1)若小明先回答 $A$ 类问题,记 $X$ 为小明的累计得分,求 $X$ 的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
某校开展"学习二十大,永远跟党走"网络知识竞赛.每人可参加多轮答题活动,每轮答题情况互不影响.每轮比赛共有两组题,每组都有两道题,只有第一组的两道题均答对,方可进行第二组答题,否则本轮答题结束。已知甲同学第一组每道题答对的概率均为 $\frac{3}{4}$ ,第二组每道题答对的概率均为 $\frac{1}{2}$ ,两组题至少答对 3 题才可获得一枚纪念章.
(1)记甲同学在一轮比赛答对的题目数为 $X$ ,请写出 $X$ 的分布列,并求 $E(X)$ ;
(2)若甲同学进行了 10 轮答题,试问获得多少枚纪念章的概率最大.
某猎人发现在距离他 100 米处的位置有一只猎物,如果直接射击,则只射击一次就击中猎物的概率为 $\frac{3}{5}$ ,为了有更大的概率击中猎物,猎人准备多次射击.假设每次射击结果之间相互独立,猎人每次射击击中猎物的概率与他和猎物之间的距离成反比.
(1)如果猎人第一次射击没有击中药物,则猎人经过调整后进行第二次射击,但由于猎物受到惊吓奔跑,使得第二次射击时猎物和他之间的距离增加了 50 米;如果第二次射击仍然没有击中猎物,则第三次射击时猎物和他之间的距离又增加了 50 米,如此进行下去,每次射击如果没有击中,则下一次射击时猎物和他之间的距离都会增加 50 米,当猎人击中猎物或发现某次射击击中的概率小于 $\frac{2}{9}$ 时就停止射击,求猎人停止射击时射击次数的概率分布列与数学期望.
(2)如果猎人直接连续射击,由于射击速度很快,可以认为在射击期间猎物和猎人之间的距离保持不变,如果希望至少击中猎物一次的概率超过 $98 \%$ ,至少要连续射击多少次?
附: $\ln 2 \approx 0.693, \ln 3 \approx 1.099, \ln 5 \approx 1.609$ .
5月25日是全国大、中学生心理健康日,"5.25"的谐音即为"我爱我",意在提醒孩子们"珍惜生命、关爱自己".学校将举行心理健康知识竞赛.第一轮选拔共设有 $A, B, C$ 三个问题,规则如下:(1)每位参加者计分器的初始分均为 10 分,答对问题 $A, B, C$ 分别加 2 分, 4 分, 5 分,答错任一题减 2 分;(2)每回答一题,计分器显示累计分数,当累计分数小于 8 分时,答题结束,淘汰出局;当累计分数大于或等于 14 分时,答题结束,进入下一轮;当答完三题,若累计分数仍不足 14 分时,答题结束,淘汰出局,若累计分数大于或等于 14 分时,答题结束,进入下一轮;(3)每位参加者按问题 $A, B, C$ 顺序作答,直至答题结束.假设甲同学对问题 $A, B, C$ 回答正确的概率依次为 $\frac{3}{4}, \frac{2}{3}, \frac{1}{2}$ ,且各题回答正确与否相互之间没有影响.
(1)求在甲同学进入下一轮的条件下,答了两题的概率;
(2)用 $\xi$ 表示甲同学本轮答题结束时答对的个数,求 $\xi$ 的分布列和数学期望 $E(\xi)$ .
哈六中举行数学竞赛,竞赛分为初赛和决赛两阶段进行.初赛采用"两轮制"方式进行,要求每个学年派出两名同学,且每名同学都要参加两轮比赛,两轮比赛都通过的同学才具备参与决赛的资格。高三学年派出甲和乙参赛.在初赛中,若甲通过第一轮与第二轮比赛的概率分别是 $\frac{2}{3}, \frac{1}{2}$ ,乙通过第一轮与第二轮比赛的概率分别是 $\frac{3}{4}, \frac{2}{3}$ ,且每名同学所有轮次比赛的结果互不影响。
(1)若高三学年获得决赛资格的同学个数为 $X$ ,求 $X$ 的分布列和数学期望.
(2)已知甲和乙都获得了决赛资格.决赛的规则如下:将问题放入 $A, B$ 两个纸箱中, A 箱中有 3 道选择题和 2道填空题,$B$ 箱中有 3 道选择题和 3 道填空题.决赛中要求每位参赛同学在 $A, B$ 两个纸箱中随机抽取两题作答.甲先从 A 箱中依次抽取 2 道题目,答题结束后将题目一起放入 $B$ 箱中,然后乙再抽取题目.已知乙从 $B$ 箱中抽取的第一题是选择题,求甲从 A 箱中抽出的是 2 道选择题的概率.
由于 $X$ 病毒正在传染蔓延,对人的身体健康造成危害,某校拟对学生被感染 $X$ 病毒的情况进行摸底调查,首先从两个班共 100 名学生中随机抽取 20 人,并对这 20 人进行逐个抽血化验,化验结果如下:
$1,9,5,6,2,3,8,5,3,4,2,6,10,5,5,2,1,7,6,6$ 。已知指数不超过 8 表示血液中不含 $X$ 病毒;指数超过 8 表示血液中含 $X$ 病毒且该生已感染 $X$ 病毒。
(1)从已获取的 20 份血样中任取 2 份血样混合,求该混合血样含 $X$ 病毒的概率;
(2)已知该校共有 1020 人,现在学校想从还未抽血化验的 1000 人中,把已感染 $X$ 病毒的学生全找出.
方案 $A$ :逐个抽血化验;
方案 $B$ :按 40 人分组,并把同组的 40 人血样分成两份,把其中的一份血样混合一起化验,若发现混合血液含 $X$ 病毒,再分别对该组的 40 人的另一份血样逐份化验;
方案 $C$ :将方案 $B$ 中的 40 人一组改为 4 人一组,其他步骤与方案 $B$ 相同。
如果用样本频率估计总体频率,且每次化验需要不少的费用.试通过计算回答:选用哪一种方案更合算?(可供参考数据: $0.9^{40} \approx 0.014,0.9^{41} \approx 0.013,0.9^4 \approx 0.656,0.9^5 \approx 0.5905$ )
甲、乙两队进行篮球比赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为"主主客客主",设甲队主场取胜的概率为 0.6 ,客场取胜的概率为 0.5 ,且各场比赛结果相互独立.
(1)在比赛进行 4 场结束的条件下,求甲队获胜的概率;
(2)赛事主办方需要预支球队费用 $a$ 万元。假设主办方在前 3 场比赛每场收入 100 万元,之后的比赛每场收入 200 万元.主办方该如何确定 $a$ 的值,才能使其获利(获利=总收入一预支球队费用)的期望高于 $a$ 万元?
袋子 A 和 $B$ 中装有若干个均匀的红球和白球,从 A 中摸一个红球的概率是 $\frac{1}{3}$ ,从 $B$ 中摸出一个红球的概率为 $p$ .
(1)从 $A$ 中有放回地摸球,每次摸出一个,有 3 次摸到红球则停止.
① 求恰好摸 5 次停止的概率;
② 记 5 次之内(含 5 次)摸到红球的次数为 $\xi$ ,求随机变量 $\xi$ 的分布列及数学期望 $E \xi$ .
(2)若 $A 、 B$ 两个袋子中的球数之比为 $1: 2$ ,将 $A 、 B$ 中的球装在一起后,从中摸出一个红球的概率是 $\frac{2}{5}$ ,求 p 的值.
甲、乙两人组成"星队"参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则"星队"得 3 分;如果只有一个人猜对,则"星队"得 1 分;如果两人都没猜对,则 "星队"得 0 分。已知甲每轮猜对的概率是 $\frac{3}{4}$ ,乙每轮猜对的概率是 $\frac{2}{3}$ ;每轮活动中甲、乙猜对与否互不影响。各轮结果亦互不影响.假设"星队"参加两轮活动,求:
(I)"星队"至少猜对 3 个成语的概率;
(II)"星队"两轮得分之和为 X 的分布列和数学期望 EX.
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过 10 分钟,如果有一个人 10 分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别 $p_1, p_2, p_3, p_2, p_3$ ,假设 $p_1, p_2, p_3$ 互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为 $q_1, q_2, q_3$ ,其中 $q_1, q_2, q_3$ 是 $p_1, p_2, p_3$ 的一个排列,求所需派出人员数目 $X$ 的分布列和均值(数字期望)$E X$ ;
(3)假定 $1>p_1>p_2>p_3$ ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为 2 元(不足 1 小时的部分按 1 小时计算)。有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为 $\frac{1}{4}, \frac{1}{2}$ ;两小时以上且不超过三小时还车的概率分别为 $\frac{1}{2}, \frac{1}{4}$ ;两人租车时间都不会超过四小时.
(I)求出甲、乙所付租车费用相同的概率;
(II)求甲、乙两人所付的租车费用之和为随机变量 $\xi$ ,求 $\xi$ 的分布列与数学期望 $E \xi$
如图, A 地到火车站共有两条路径 $L_1$ 和 $L_2$ ,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
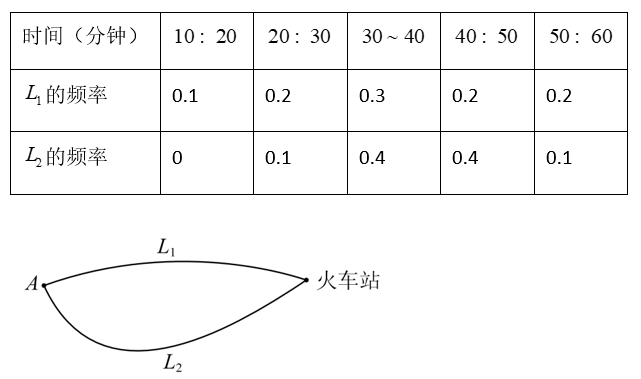
现甲、乙两人分别有 40 分钟和 50 分钟时间用于赶往火车站.
(I)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(II)用 X 表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(I)的选择方案,求 X 的分布列和数学期望。
一批产品需要进行质量检验,检验方案是:先从这批产品中任取 4 件作检验,这 4 件产品中优质品的件数记为 $n$ .如果 $n=3$ ,再从这批产品中任取 4 件作检验,若都为优质品,则这批产品通过检验;如果 $n=4$ ,再从这批产品中任取 1 件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为 $50 \%$ ,即取出的产品是优质品的概率都为 $50 \%$ ,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为 100 元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为 $X$(单位:元),求 $X$ 的分布列及数学期望.
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 $\frac{2}{3}$ ,中奖可以获得 2分;方案乙的中奖率为 $\frac{2}{5}$ ,中奖可以获得 3 分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
(I)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为 $X$ ,求 $X \leq 3$ 的概率;
(II)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为 $0.5,0.6,0.4$ .经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为 $0.6,0.5,0.75$ .
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为 $\xi$ ,求随机变量 $\xi$ 的期望.
先在甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 $\frac{3}{4}$ ,命中得 1 分,没有命中得 0 分;向乙靶射击两次,每次命中的概率为 $\frac{2}{3}$ ,每命中一次得 2 分,没有命中得 0 分。该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中一次的概率;
(II)求该射手的总得分 $X$ 的分布列及数学期望 $E X$ .
因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出两种拯救果树的方案,每种方案都需分两年实施.若实施方案一,预计第一年可以使柑桔产量恢复到灾前的 1.0 倍、 0.9 倍、 0.8 倍的概率分别是 $0.3 、 0.3 、 0.4$ ;第二年可以使柑桔产量为第一年产量的 1.25 倍、 1.0 倍的概率分别是 $0.5 、 0.5$ .若实施方案二,预计第一年可以使柑桔产量达到灾前的 1.2 倍、 1.0 倍、 0.8 倍的概率分别是 $0.2 、 0.3 、 0.5$ ;第二年可以使柑桔产量为第一年产量的 1.2 倍、 1.0 倍的概率分别是 $0.4 、 0.6$ .实施每种方案第一年与第二年相互独立,令 $\xi_i(i=1,2)$ 表示方案 $i$ 实施两年后柑桔产量达到灾前产量的倍数.
(1)写出 $\xi_1 、 \xi_2$ 的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到、恰好达到、超过灾前产量,预计利润分别为 10 万元、 15 万元、20 万元.问实施哪种方案的平均利润更大?