单选题 (共 11 题 ),每题只有一个选项正确
复平面内, 复数 $(1-2 i)(2+i)$ 的对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知集合 $M, N$ 满足 $M \cap N=N$, 则
$\text{A.}$ $M=N$
$\text{B.}$ $M=\varnothing$
$\text{C.}$ $M \supseteq N$
$\text{D.}$ $M \subseteq N$
已知直线 $l: y=2 x+b$ 与圆 $C:(x+2)^2+(y-3)^2=5$ 有公共点, 则 $b$ 的取值范围为
$\text{A.}$ $[2,12]$
$\text{B.}$ $(-\infty, 2] \cup[12,+\infty)$
$\text{C.}$ $[-4,6]$
$\text{D.}$ $(-\infty,-4] \mathrm{U}[6,+\infty)$
已知函数 $f(x)=\left\{\begin{array}{l}\sin x, x \leq 0 \\ f\left(x-\frac{\pi}{2}\right)+m, x>0\end{array}\right.$ 满足 $f(\pi)=1$, 则实数 $m$ 的值为
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 的 8 个顶点中任取 4 个点, 能构成正三棱椎的个数为
$\text{A.}$ 16 个
$\text{B.}$ 12 个
$\text{C.}$ 10 个
$\text{D.}$ 8 个
已知函数 $f(x)=x \lg \frac{x+m}{x-3}$ 是偶函数, 则 $m=$
$\text{A.}$ 3
$\text{B.}$ 0
$\text{C.}$ -1
$\text{D.}$ 2
已知函数 $f(x)=\sin \pi x, x \in(0,2)$ 的图象与直线 $y=a(x-1)$ 有 3 个交点, 则实数 $a$ 的取值范围为
$\text{A.}$ $(-\infty, 0)$
$\text{B.}$ $(-1,0)$
$\text{C.}$ $(-\infty,-\pi)$
$\text{D.}$ $(-\pi, 0)$
已知双曲线: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点为 $F_1, F_2,\left|F_1 F_2\right|=2 a+2, P$ 为双曲线右支上一点, $P F_2 \perp F_1 F_2, \triangle P F_1 F_2$ 的内切圆圆心为 $M, \triangle M F_1 P$ 与 $\mathrm{V}_2 P$ 的面积的差为 1 , 则双曲线的离心率 $e=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\sqrt{5}$
已知 $m, n$ 都是正整数, 且 $m < n$, 下列有关组合数的计算, 正确的是
$\text{A.}$ $C_n^m=C_n^{n-m}$
$\text{B.}$ $C_{n-1}^m+C_{n-1}^{m-1}=C_n^{m+1}$
$\text{C.}$ $m C_n^m=n C_{n-1}^{m-1}$
$\text{D.}$ $\left(C_n^0\right)^2+\left(C_n^1\right)^2+\cdots+\left(C_n^n\right)^2=C_{2 n}^n$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}$, 则以下选项正确的是
$\text{A.}$ 若 $f(x+1)=-f(x)$, 则 $f(x+2)=f(x)$
$\text{B.}$ 若 $f(x+2)=f(x)$, 则 $f(x+1)=-f(x)$
$\text{C.}$ 若 $f(x+2)=f(-x)$, 且 $f(x)$ 为奇函数, 则 $f(x+4)=f(x)$
$\text{D.}$ 若 $f(x+2)=f(-x)$, 且 $f(x+4)=f(x)$, 则 $f(x)$ 为奇函数
数列 $\left\{a_n\right\}$ 的通项公式为 $a_n=\left(1+\frac{1}{n}\right)^n$, 下列命题正确的为
$\text{A.}$ $\left\{a_n\right\}$ 先递增后递减
$\text{B.}$ $\left\{a_n\right\}$ 为递增数列
$\text{C.}$ $\exists n \in \mathbf{N}^*, a_n>e$
$\text{D.}$ $\forall n \in \mathbf{N}^*, a_n < e$
多选题 (共 1 题 ),每题有多个选项正确
如图, 正三棱柱 $A B C-A_1 B_1 C_1$ 的各条棱长都为 $2, M, N$ 分别是 $A B, A_1 C_1$ 的中点, 则

$\text{A.}$ $M N \perp A C$
$\text{B.}$ $M N / / B C_1$
$\text{C.}$ $M N=\sqrt{5}$
$\text{D.}$ $M N / /$ 平面 $B C C_1 B_1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知向量 $\vec{a}=(x, 3), \vec{b}=(2,6)$, 若 $\vec{a}$ 与 $\vec{b}$ 共线, 则实数 $x=$
已知圆雉的侧面展开图是半径为 8 的直角扇形, 则此圆雉的表面积为
已知抛物线 $E: y^2=4 x$, 圆 $M:(x-1)^2+y^2=1$, 过点 $M$ 的直线 $l$ 与 $E$ 交于 $A, B$ 两点, 与圆 $M$ 交于 $C, D$两点 ( $A, C$ 都在 $x$ 轴上方), 若 $|A C|-|B D|=2 \sqrt{3}$, 则直线 $l$ 的斜率为
已知函数 $f(x)=\cos (\omega x+\varphi)(\omega>0), A, B$ 是直线 $y=\frac{1}{2}$ 与曲线 $f(x)$ 的两个交点, 若 $|A B|$ 的最小值为 $\frac{\pi}{6}$, $f\left(\frac{2 \pi}{3}\right)=0, f(0) < 0$, 则 $f\left(\frac{\pi}{3}\right)=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c, \sqrt{3} a \sin B+a \cos B=b+c$
(1) 求 $A$;
(2) 设 $A C$ 边的中线 $B D=\sqrt{13}$, 且 $a^2+c^2=28$, 求 $\triangle A B C$ 的面积 $S$.
目前, 国际上常用身体质量指数 (Body Mass Index, 缩写 BMI) 来测量人体胖瘦程度以及是否健康, 其计算公式是 ${B M I}=\frac{\text { 体重 }(\text { 单位 } \cdot \mathrm{kg})}{\text { 身高 }^2\left(\text { 单位 } m^2\right)}$. 中国成人的 BMI 数值标如下表所示:

为了解某单位职工的身体情况,研究人员从单位职工体检数据中,采用分层随机抽样方法抽取了90名男职工、50名女职工的身高和体重数据,计算得到他们的BMI值,并进行分类统计,如右表所示:
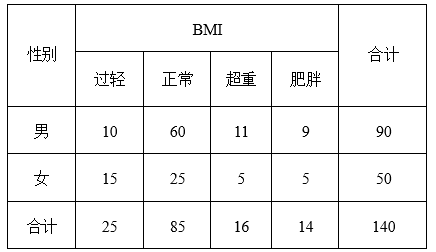
(1)参照附表,对小概率值a逐一进行独立性检验,依据检验,指出能认为职工体重是否正常与性别有关联的a的一个值;
(2)在该单位随机抽取一位职工的BMI值,发现其BMI值不低于28.由上表可知男女职工的肥胖率都为0.1,视频率为概率,能否认为该职工的性别是男还是女的可能性相同?若认为相同则说明理由,若认为不相同,则需要比较可能性的大小

记 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 当 $n \geq 2$ 时, $a_n=\left\{\begin{array}{c}a_{n-1}+1, n \text { 为奇数 } \\ 2 a_{n-1}, n \text { 为偶数 }\end{array}\right.$. 且 $S_3=1$.
(1) 求 $a_1, a_2$;
(2)
(i) 当 $n$ 为偶数时, 求 $\left\{a_n\right\}$ 的通项公式;
(ii) 求 $S_{2024}$.
如图, 在四棱椎 $P-A B C D$ 中, $P C \perp$ 底面 $A B C D, A B \perp A D, B C / / A D, A D=2 A B=2 B C=2, P C=3$, $\overrightarrow{P E}=\lambda \overrightarrow{P D}(0 < \lambda < 1)$
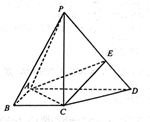
(1) 求证: $C D \perp P A$;
(2) 若平面 $P A C$ 与平面 $E A C$ 夹角的余弦值为 $\frac{3 \sqrt{17}}{17}$, 求三棱雉 $P-A C E$ 的体积.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的右焦点为 $F(2,0)$, 点 $M(\sqrt{6}, 1)$ 在椭圆上.
(1) 求椭圆 $C$ 的方程;
(2) 直线 $l: y=k x+m$ 与 $C$ 相交于 $A, B$ 两点, 若直线 $A F, B F$ 的倾斜角互补, 求 $\triangle A B F$ 面积的最大值.
已知函数 $f(x)=e^x-\ln (x+m)-m(m \in \mathbf{R})$.
(1) 若 $m=1$, 求函数 $f(x)$ 的极值;
(2) 若 $f(x)$ 有两个零点, 求 $m$ 的取值范围.