单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \mid x^2-2 x-8 < 0\right\}, B=\{-2,-1,0,1,2\}$, 则 $A \cap B=$
$\text{A.}$ $\{-2,-1,0,1,2\}$
$\text{B.}$ $\{-1,0,1,2\}$
$\text{C.}$ $\{-1,0,1\}$
$\text{D.}$ $\{-2,-1,0,1\}$
复数 $z=\frac{2-\mathrm{i}}{2+\mathrm{i}}$, 则 $z-\bar{z}=$
$\text{A.}$ $-\frac{6}{5}$
$\text{B.}$ $\frac{6}{5}$
$\text{C.}$ $-\frac{8}{5} \mathrm{i}$
$\text{D.}$ $\frac{8}{5} \mathrm{i}$
两个单位向量 $e_1$ 与 $e_2$ 满足 $e_1 \cdot e_2=0$, 则向量 $e_1-\sqrt{3} e_2$ 与 $e_2$ 的夹角为
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $150^{\circ}$
要得到函数 $f(x)=\sin \left(2 x+\frac{\pi}{3}\right)$ 的图象, 可以将函数 $g(x)=\sin \left(2 x+\frac{\pi}{12}\right)$ 的图象
$\text{A.}$ 向左平移 $\frac{\pi}{4}$ 个単位
$\text{B.}$ 向左平移 $\frac{\pi}{8}$ 个单位
$\text{C.}$ 向右平移 $\frac{\pi}{4}$ 个単位
$\text{D.}$ 向右平移 $\frac{\pi}{8}$ 个单位
某玻璃制品厂需要生产一种如图 1 所示的玻璃杯, 该玻璃杯造型可以近似看成是一个 圆柱挖去一个圆台得到, 其近似模型的直观图如图 2 所示 (图中数据单位为 $\mathrm{cm}$ ), 则该 坡璃杯近似模型的体积 (单位: $\mathrm{cm}^3$ ) 为
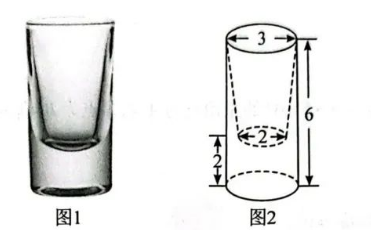
$\text{A.}$ $\frac{43 \pi}{6}$
$\text{B.}$ $\frac{47 \pi}{6}$
$\text{C.}$ $\frac{51 \pi}{6}$
$\text{D.}$ $\frac{55 \pi}{6}$
某企业在生产中为倡导绿色环保的理念, 购人污水过滤系统对污水进行过滤处理, 已知 在过滤过程中污水中的剩余污染物数量 $N(\mathrm{mg} / \mathrm{L})$ 与时间 $t(\mathrm{~h})$ 的关系为 $N=N_0 e^{-k t}$, 其 中 $N_0$ 为初始污染物的数量, $k$ 为常数. 若在某次过滤过程中, 前 2 个小时过滤掉了污染 物的 $30 \%$, 则可计算前 6 小时共能过滤掉污染物的
$\text{A.}$ $49 \%$
$\text{B.}$ $51 \%$
$\text{C.}$ $65.7 \%$
$\text{D.}$ $72.9 \%$
过双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点 $F$ 作圆 $x^2+y^2=a^2$ 的一条切线, 设切点为 $T$, 该切线与双曲线 $E$ 在第一象限交于点 $A$, 若 $\overrightarrow{F A}=3 \overrightarrow{F T}$, 则双曲线 $E$ 的离心率为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $\frac{\sqrt{13}}{2}$
$\text{D.}$ $\frac{\sqrt{15}}{2}$
已知 $A, B, C, D$ 是半径为 $\sqrt{5}$ 的球体表面上的四点, $A B=2, \angle A C B=90^{\circ}, \angle A D B=30^{\circ}$, 则 平面 $C A B$ 与平面 $D A B$ 的夹角的余弦值为
$\text{A.}$ $\frac{\sqrt{6}-\sqrt{2}}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
多选题 (共 4 题 ),每题有多个选项正确
四个实数 $-1,2, x, y$ 按照一定顺序可以构成等比数列, 则 $x y$ 的可能取值有
$\text{A.}$ $-\frac{1}{8}$
$\text{B.}$ -2
$\text{C.}$ -16
$\text{D.}$ -32
直线 $y=k x-k$ 过抛物线 $E: y^2=2 p x(p>0)$ 的焦点且与该抛物线交于 $M, N$ 两点, 设 $O$ 为坐标原点, 则下列说法中正确的是
$\text{A.}$ $p=1$
$\text{B.}$ 抛物线 $E$ 的准线方程是 $x=-1$
$\text{C.}$ 以 $M N$ 为直径的圆与定直线相切
$\text{D.}$ $\angle M O N$ 的大小为定值
已知实数 $a, b$ 满足 $a \mathrm{e}^a=b \ln b=3$, 则
$\text{A.}$ $a=\ln b$
$\text{B.}$ $a b=\mathrm{e}$
$\text{C.}$ $b-a < \mathrm{e}-1$
$\text{D.}$ $\mathrm{e}+1 < a+b < 4$
若函数 $f(x)=\cos 2 x-\cos x+k$ 存在连续四个相邻且依次能构成等差数列的零点, 则实 数 $k$ 的可能取值有
$\text{A.}$ -2
$\text{B.}$ $\frac{9}{8}$
$\text{C.}$ 0
$\text{D.}$ $\frac{1}{2}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$(x+1)(1-2 x)^5$ 的展开式中含 $x^3$ 项的系数为
圆心在直线 $x+y-1=0$ 上且与直线 $2 x-y-1=0$ 相切于点 $(1,1)$ 的圆的方程 是
若函数 $f(x)=(2 x+1) \ln x-a x$ 是 $(0,+\infty)$ 上的增函数, 则实数 $a$ 的最大值 为
甲, 乙, 丙三人进行传球游戏,每次投郑一枚质地均匀的正方体骰子决定传球的方式: 当球在甲手中时, 若骰子点数大于 3 , 则甲将球传给乙, 若点数不大于 3 , 则甲将球保 留; 当球在乙手中时, 若骰子点数大于 4 , 则乙将球传给甲, 若点数不大于 4 , 则乙将球 传给丙; 当球在丙手中时, 若骰子点数大于 3 , 则丙将球传给甲, 若骰子点数不大于 3 , 则丙将球传给乙. 初始时, 球在甲手中, 投掷 $n$ 次骰子后 $\left(n \in N^*\right)$, 记球在甲手中的概 率为 $p_n$, 则 $p_3=$ $; p_n=$ . (第一空 2 分,第二空 3 分)
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
记数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 对任意正整数 $n$, 有 $2 S_n=(n+2)\left(a_n-1\right)$.
(1) 证明: 数列 $\left\{\frac{a_n+1}{n+1}\right\}$ 为常数列;
(2) 求数列 $\left\{\frac{1}{a_n a_{n+1}}\right\}$ 的前 $n$ 项和 $T_n$.
设 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为 $a, b, c$, 且 $2 a \cos B=2 c-b$.
(1) 求角 $A$;
(2) 若 $a=7$, 且 $\triangle A B C$ 的内切圆半径 $r=\sqrt{3}$, 求 $\triangle A B C$ 的面积 $S$.
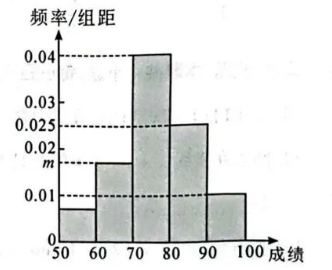
近期世界地震、洪水、森林大火等自然灾害频繁出现, 紧急避险知识越来越引起人们的 重视. 某校为考察学生对紧急避险知识的掌握情况, 从全校学生中选取 200 名学生进 行紧急避险知识测试, 其中男生 110 名,女生 90 名. 所有学生的测试成绩都在区间 $[50,100]$ 范围内, 由测试成绩数据作出如图所示 的频率分布直方图.
(1) 若从频率分布直方图中估计出样本的平均数 与中位数相等, 求图中 $m$ 的值;
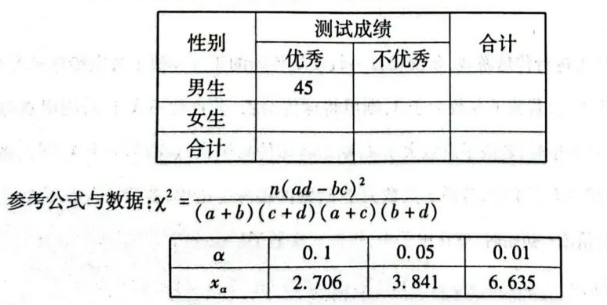
(2) 规定测试成绩不低于 80 分为优秀, 已知共有 45 名男生成绩优秀, 完成下面的列联表, 并 根据小概率值 $\alpha=0.05$ 的独立性检验, 能否 推断男生和女生的测试成绩优秀率有差异?
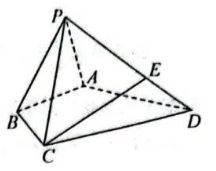
如图, 在四棱锥 $P-A B C D$ 中, 底面四边形 $A B C D$ 满足 $A B=C B=\sqrt{2}, A D=C D=\sqrt{5}$, $\angle A B C=90^{\circ}$, 棱 $P D$ 上的点 $E$ 满足 $P E=2 D E$.
(1) 证明: 直线 $C E / /$ 平面 $P A B$;
(2) 若 $P B=\sqrt{5}, P D=2 \sqrt{2}$, 且 $P A=P C$, 求直线 $C E$ 与平面 $P B C$ 所成角的正弦值.
椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左顶点为 $A$, 右顶点为 $B$, 满足 $|A B|=4$, 且椭圆 $E$ 的离 心率为 $\frac{\sqrt{3}}{2}$.
(1) 求椭圆 $E$ 的标准方程;
(2) 已知点 $T\left(t, \frac{1}{2}\right)$ 在椭圆 $E$ 的内部, 直线 $A T$ 和直线 $B T$ 分别与椭圆 $E$ 交于另外的点 $C$ 和点 $D$, 若 $\triangle C D T$ 的面积为 $\frac{1}{17}$, 求 $t$ 的值.
已知函数 $f(x)=\left(x^2+m x+n\right) \mathrm{e}^x$.
(1) 若 $m=n=0$, 求 $f(x)$ 的单调区间;
(2) 若 $m=a+b+2, n=a^2+b^2+2$, 且 $f(x)$ 有两个极值点, 分别为 $x_1$ 和 $x_2\left(x_1 < x_2\right)$, 求 $\frac{f\left(x_2\right)-f\left(x_1\right)}{\mathrm{e}^{x_2}-\mathrm{e}^{x_1}}$ 的最小值.