单选题 (共 8 题 ),每题只有一个选项正确
设复数 $z$ 满足 $z=\frac{\bar{z}-1}{2}$, 则 $|z|=$
$\text{A.}$ 2
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ 1
$\text{D.}$ $\frac{1}{2}$
已知集合 $A=\{1,3, \sqrt{m}\}, B=\{1, m\}$, 若 $B \subseteq A$, 则 $m=$
$\text{A.}$ 1
$\text{B.}$ 0 或 1 或 3
$\text{C.}$ 0 或 3
$\text{D.}$ 1 或 3
已知 $m, n$ 表示空间内两条不同的直线, 则使 $m // n$ 成立的必要不充分条件是
$\text{A.}$ 存在平面 $\alpha$, 有 $m\|\alpha, n\| \alpha$
$\text{B.}$ 存在平面 $\alpha$, 有 $m \perp \alpha, n \perp \alpha$
$\text{C.}$ 存在直线 $l$, 有 $m \perp l, n \| l$
$\text{D.}$ 存在直线 $l$, 有 $m\|l, n\| l$
“锦里开芳宴, 兰缸艳早年.”元宵节是中国非常重要的传统节日, 某班级准备进行“元宵福气到”抽 奖活动福袋中装有标号分别为 $1,2,3,4,5$ 的五个相同小球, 从袋中一次性摸出三个小 球, 若号码之和是 3 的倍数, 则获奖. 若有 5 名同学参与此次活动, 则恰好 3 人获奖的概率是
$\text{A.}$ $\frac{72}{625}$
$\text{B.}$ $\frac{108}{625}$
$\text{C.}$ $\frac{144}{625}$
$\text{D.}$ $\frac{216}{625}$
已知双曲线 $\frac{x^2}{4}-\frac{y^2}{5}=1$ 的左、右焦点分别为 $F_1, F_2$, 点 $P\left(3, \frac{5}{2}\right)$, 则 $\angle F_1 P F_2$ 的平分线的方程为
$\text{A.}$ $3 x-2 y-4=0$
$\text{B.}$ $3 x-4 y+4=0$
$\text{C.}$ $4 x-6 y+3=0$
$\text{D.}$ $2 x-6 y+9=0$
若不等式 $\sqrt{16-x^2} \leq k x(k>0)$ 的解集为区间 $[a, b]$, 且 $b-a=2$,则 $k=$
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 2
如图, 在边长为 2 的等边 $\triangle A B C$ 中, 点 $E$ 为中线 $B D$ 的三等分点 (靠近点 $B$ ), 点 $F$ 为 $B C$ 的中点, 则 $\overrightarrow{F E} \cdot \overrightarrow{E C}=(\quad) \mid$
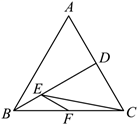
$\text{A.}$ $-\frac{\sqrt{3}}{4}$
$\text{B.}$ $-\frac{5}{6}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{1}{2}$
若函数 $f(x)=\sqrt{\frac{1}{2} x+a^2}+\sqrt{x^2-1}-x$ 有零点, 则 $a$ 的取值范围是
$\text{A.}$ $\left[-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right]$
$\text{B.}$ $\left(-\infty,-\frac{\sqrt{2}}{2}\right) \cup\left(\frac{\sqrt{2}}{2},+\infty\right)$
$\text{C.}$ $\left(0, \frac{1}{2}\right)$
$\text{D.}$ $\left(\frac{1}{2},+\infty\right)$
多选题 (共 4 题 ),每题有多个选项正确
2017年全国居民恩格尔系数为$29.39 \%$,这是历史上中国恩格尔系数首次跌破30%.恩格尔系数是由德国统计学家恩斯特·恩格尔提出的,计算公式是 $ 恩格尔系数=\dfrac{食物支出金额}{ 总支出金额} \times 100 \% $
恩格尔系数是国际上通用的衡量居民生活水平高低的一项重要指标,一般随居民家庭收入和生活水平的提高而下降,恩格尔系数达60%以上为贫困,$50 \%~60 \%$为温饱,$40 \%~50 \%$为小康,$30 \%~40 \%$ 为富裕,低于$30 \%$为最富裕.如图是近十年我国农村与城镇居民的恩格尔系数折线图,由图可知
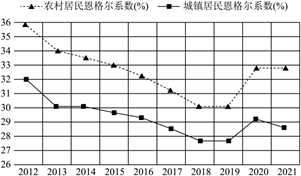
$\text{A.}$ 城镇居民2015年开始进入“最富裕”水平
$\text{B.}$ 农村居民恩格尔系数的平均数低于$32 \%$
$\text{C.}$ 城镇居民恩格尔系数的第45百分位数高于$29 \%$
$\text{D.}$ 全国居民恩格尔系数等于农村居民恩格尔系数和城镇居民恩格尔系数的平均数
将函数 $f(x)=\sin (2 x+\varphi)\left(|\varphi| < \frac{\pi}{2}\right)$ 的图象向左平移 $\frac{\pi}{4}$ 个单位得到函数 $g(x)$ 的图象, 若 $g(x)$ 的图象 与 $f(x)$ 的图象关于 $y$ 轴对称, 则下列说法正确的有
$\text{A.}$ $\varphi=\frac{\pi}{4}$
$\text{B.}$ 函数 $f(x)$ 图象的对称轴过函数 $g(x)$ 图象的对称中心
$\text{C.}$ 在区间 $\left[-\frac{\pi}{8}, \frac{\pi}{8}\right]$ 上, 函数 $g(x)$ 与 $f(x)$ 都单调递减
$\text{D.}$ $\forall m \in\left[-\frac{\pi}{4}, \frac{\pi}{8}\right], \exists n \in\left[-\frac{\pi}{4}, \frac{\pi}{8}\right]$, 使得 $g(m)=f(n)$
已知 $F$ 是抛物线 $y^2=2 p x,(p>0)$ 的焦点, 过 $F$ 的直线交抛物线于 $A, B$ 两点, 以线段 $A B$ 为直径的虽交 $y$ 轴于 $M, N$ 两点, 交准线 $l$ 于 $Q$ 点, 则下列说法正确的是
$\text{A.}$ 以 $A F$ 为直径的圆与 $y$ 轴相切
$\text{B.}$ 若抛物线上的点 $T(1, t)$ 到 $F$ 的距离为 2 , 则抛物线的方程为 $y^2=2 x$
$\text{C.}$ $\overrightarrow{A Q} \cdot \overrightarrow{B Q}=0$
$\text{D.}$ $|M N|$ 的最小值为 $2 p$
下列不等关系中, 正确的是
$\text{A.}$ $\ln 2 < \frac{2}{e}$
$\text{B.}$ $\frac{\ln ^3}{\ln ^\pi} < \frac{3}{\pi}$
$\text{C.}$ $\frac{e}{2}>\ln ^3$
$\text{D.}$ $\sqrt{e}>2-\ln ^2$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$\left(x+\frac{1}{x}+2\right)^4$ 的展开式的常数项是
我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为 ________ 日.
(结果保留一位小数,参考数据:lg2≈0.30,lg3≈0.48)
若过点 $A(a, 2 a)$ 与曲线 $f(x)=x \ln x$ 相切的直线有两条, 则实数 $a$ 的取值范围是
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $1, P$ 是空间中任意一点. 给出下列四个结论:
(1)若点 $P$ 在线段 $A D_1$ 上运动, 则始终有 $C_1 P \perp C B_1$;
(2)若点 $P$ 在线段 $A A_1$ 上运动, 则过 $P, B, D_1$ 三点的正方体截面面积的最小值为 $\frac{\sqrt{6}}{4}$;
(3)若点 $P$ 在线段 $A D_1$ 上运动, 三棱锥 $D-B P C_1$ 体积为定值;
(4) 若点 $P$ 在线段 $A_1 B$ 上运动, 则 $A P+P D_1$ 的最小值为 $\sqrt{2+\sqrt{2}}$.
其中所有正确结论的序号有
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, $a 、 b 、 c$ 分别是角 $A 、 B 、 C$ 的对边, $\frac{c}{a+b}+\frac{a}{b+c}=1$.
(1)求 $B$ 的大小;
(2)若 $b=2$, 求 $\triangle A B C$ 的周长 $L$ 的取值范围.
设 $S_n$ 为等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 其中 $a_1=1$, 且 $\frac{S_n}{a_n}=\lambda a_{n+1}\left(n \in \boldsymbol{N}^*\right)$.
(1) 求常数 $\lambda$ 的值, 并写出 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $T_n$ 为数列 $\left\{\left(-\frac{1}{2}\right)^{a_n}\right\}$ 的前 $n$ 项和, 若对任意的 $n \in N^*$, 都有 $\left|p T_n-2\right| \leq 1$, 求实数 $p$ 的取值范 围。
某乡镇全面实施乡村振兴, 大力发展特色产业——富硒水果. 工作人员统计了近 8 年富硒水果种植 面积 $x_i$ (单位: 百亩) 与年销售额 $y_i$ (单位: 千万元) 的数据 $(i=1,2,3, \cdots, 8)$. 经计算得到如下处 理后的统计量: $\bar{x}=3.1, \bar{y}=30, \bar{w}=3.24, \sum_{i=1}^8 x_i w_i=86.82, \sum_{i=1}^8 x_i^2=93.88$,
$$
\begin{aligned}
& \sum_{i=1}^8 w_i^2-8 \bar{w}^2=2.7, \sum_{i=1}^8 v_i y_i=3974.5, \sqrt{\left(\sum_{i=1}^8 v_i^2-8 \bar{v}^2\right)\left(\sum_{i=1}^8 y_i^2-8 \bar{y}^2\right)}=1162.4, \\
& \sum_{i=1}^8 v_i^2-8 \bar{v}^2=630.3, \text { 其中 } w_i=\ln y_i, \quad v_i=x_i^2(i=1,2,3, \cdots, 8) .
\end{aligned}
$$
(1)根据以上数据, 从相关系数的角度, 判断 $y=a x^2+b$ 与 $y=e^{c x+d}$ 哪个适宜作为年销售额 $y$ 关于 种植面积 $x$ 的回归方程类型 (相关系数精确到 0.01).
(2)根据 (1) 的判断结果及相关数据, 建立 $y$ 关于 $x$ 的回归方程 (系数精确到 0.01).
(3)该乡镇计划年销售额不低于 10 亿元, 请预测种植面积至少为多少亩.
附: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$, 回归直线 $\hat{y}=\hat{\alpha} x+\hat{\beta}$ 的斜率与截距的最小二乘估计分别为 $\hat{\alpha}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{\beta}=\bar{y}-\hat{\alpha} \bar{x}$.
参考数据: $\sqrt{49.78} \approx 7.06, \sqrt{45.9} \approx 6.77$.
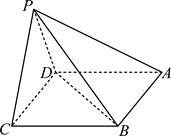
如图, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为菱形, $\triangle P C D$ 是边长为 2 的正三角形, $\angle B C D=60^{\circ}$.
(1)求证: $A B \perp B P$;
(2) 若四棱雉 $P-A B C D$ 的体积为 2 , 求二面角 $A-P D-C$ 的余弦值.
$P$ 为圆 $A:(x+2)^2+y^2=36$ 上一动点, 点 $B$ 的坐标为 $(2,0)$, 线段 $P B$ 的垂直平分线交直线 $A P$ 于点 $Q$.
(1)求点 $Q$ 的轨迹方程 $C$;
(2) 在 (1) 中曲线 $C$ 与 $x$ 轴的两个交点分别为 $A_1$ 和 $A_2, M 、 N$ 为曲线 $C$ 上异于 $A_1 、 A_2$ 的两点, 直线 $M N$ 不过坐标原点, 且不与坐标轴平行. 点 $M$ 关于原点 $O$ 的对称点为 $S$, 若直线 $A_1 S$ 与直线 $A_2 N$ 相交 于点 $T$, 直线 $O T$ 与直线 $M N$ 相交于点 $R$, 证明: 在曲线 $C$ 上存在定点 $E$, 使得 $\triangle R B E$ 的面积为定值, 并求该定值.
已知函数 $f(x)=x^2-a_{\ln }(1-x), a \in R$.
(1)讨论函数 $f(x)$ 的单调性;
(2) 若函数 $f(x)$ 有两个极值点 $x_1, x_2$, 且 $x_1 < x_2$, 求证: $2 f\left(x_1\right)-a x_2>\left(2 \ln ^2-\frac{3}{2}\right) a$.