单选题 (共 14 题 ),每题只有一个选项正确
2022 的相反数
$\text{A.}$ $\frac{1}{2022}$
$\text{B.}$ $-\frac{1}{2022}$
$\text{C.}$ 2022
$\text{D.}$ -2022
下列运算正确的是
$\text{A.}$ $2 x+y=2 x y$
$\text{B.}$ $x^2 \cdot x^3=x^6$
$\text{C.}$ $2 x^6 \div x^2=2 x^4$
$\text{D.}$ $4 x-5 x=-1$
某中学篮球队12名队员的年龄情况如下表,则这个队队员年龄的众数和中位数分别

$\text{A.}$ 15,16
$\text{B.}$ 15,15
$\text{C.}$ 15,15.5
$\text{D.}$ 16,15
国家卫健委网站消息:截至2022年5月27日,31个省 (自治区,直辖市) 和新疆生产建设兵团累计报告接种 新冠病毒疫苗超过33亿剂次,用科学记数法表示33亿是
$\text{A.}$ $3.3 \times 10^8$
$\text{B.}$ $33 \times 10^8$
$\text{C.}$ $3.3 \times 10^9$
$\text{D.}$ $3.3 \times 10^{10}$
已知 $\angle \alpha=76^{\circ} 22^{\prime}$ ,则 $\angle \alpha$ 的补角是
$\text{A.}$ $103^{\circ} 38^{\prime}$
$\text{B.}$ $103^{\circ} 78^{\prime}$
$\text{C.}$ $13^{\circ} 38^{\prime}$
$\text{D.}$ $13^{\circ} 78^{\prime}$
已知一个底面半径为 $3 \mathrm{~cm}$ 的圆锥,它的母线长是 $5 \mathrm{~cm}$ ,则这个圆雉的侧面积是 ( ) $\mathrm{cm}^2$
$\text{A.}$ $15 \pi$
$\text{B.}$ $45 \pi$
$\text{C.}$ $30 \pi$
$\text{D.}$ $20 \pi$
北京2022冬奧会吉样物“冰墩墩”和“雪容融”受到大家的喜爱,某网店出售这两种吉祥物礼品,借价如图 所示.小明妈妈一共买10件礼品,总共花费不超过 900 元,如果设购买冰墩墩礼品 $x$ 件,则能够得到的不等式是

$\text{A.}$ $100 x+80(10-x)>900$
$\text{B.}$ $100 x+80(10-x) < 900$
$\text{C.}$ $100 x+80(10-x) \geq 900$
$\text{D.}$ $100 x+80(10-x) \leq 900$
在数轴上,点 $\mathrm{A}$ 所表示的实数为 4 ,点 $\mathrm{B}$ 所表示的实数为 $\mathrm{b} , \odot A$ 的半径为 2 ,要使点 $\mathrm{B}$ 在 $\odot A$ 内时,实数 $\mathrm{b}$ 的取 值范围是
$\text{A.}$ $b>2$
$\text{B.}$ $b>6$
$\text{C.}$ $b < 2$ 或 $b>6$
$\text{D.}$ $2 < b < 6$
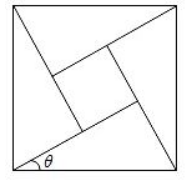
公元三世纪,我国汉代数学家赵爽在注解 《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等 的直角三角形与中间的小正方形拼成的一个大正方形. 如果大正方形的面积是 125 ,小正方形面积是 25 ,则 $(\sin \theta+\cos \theta)^2= $
$\text{A.}$ $\frac{9}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{5}$
$\text{C.}$ $\frac{3 \sqrt{5}}{5}$
$\text{D.}$ $\frac{1}{5}$
. 中国抗击疫情最宝贵的经验就是“早发现,早报告,早隔离,早治疗”。在这 12 个字中“早”字出现的频率 是
$\text{A.}$ $\frac{1}{12} $
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{1}{3}$
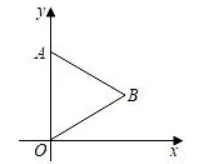
如图, 将等边 $\triangle A O B$ 放在平面直角坐标系中, 点 $A$ 的坐标为 $(0,4)$, 点 $B$ 在第一象限, 将等边 $\triangle A O B$ 绕 点 $O$ 顺时针旋堑 $180^{\circ}$ 得到 $\triangle A^{\prime} O B^{\prime}$ ,则点 $B$ 的对应点 $B^{\prime}$ 的坐标是
$\text{A.}$ $(2 \sqrt{3}, 2)$
$\text{B.}$ $(2 \sqrt{3},-2)$
$\text{C.}$ $(-2 \sqrt{3},-2)$
$\text{D.}$ $(0,-4)$
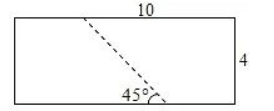
如图,将边长分别为10cm和4cm的矩形纸片沿着虚线剪成两个全等的梯形纸片.裁剪线与矩形较长边所夹的锐角是45°,则梯形纸片中较短的底边长为
$\text{A.}$ 2cm
$\text{B.}$ 2.5cm
$\text{C.}$ 3cm
$\text{D.}$ 3.5cm
如图,抛物线 $y=a x^2+b x+1$ 的顶点在直线 $y=k x+1$ 上,对称轴为直线 $x=1$, 有以下四个结论: (1) $a b < $ 0 , (2) $b < \frac{1}{3}$, (3) $a=-k$, (4) 当 $0 < x < 1$ 时, $a x+b>k$, 其中正确的结论是

$\text{A.}$ ①②③
$\text{B.}$ ①③④
$\text{C.}$ ①②④
$\text{D.}$ ②③④
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若二次根式 $\sqrt{x+1}$ 有意义, 则 $x$ 的取值范围是
不等式组 $\left\{\begin{array}{l}-x+4 < 2 \\ x-3 \leqslant 2\end{array}\right.$ 的解集为
已知样本 $1,3,9, a, b$ 的众数是9, 平均数是 6 , 则中位数为
如图,在四边形 $A B C D$ 中, $A D // B C, \angle A=R t \angle, A D=2 \mathrm{~cm}, A B=4 \mathrm{~cm}, B C=6 \mathrm{~cm}$, 点 $E$ 是 $C D$ 中点, 过点 $B$ 画射线 $B F$ 交 $C D$ 于点 $F$, 交 $A D$ 延长线于点 $G$, 且 $\angle G B E=\angle C B E$, 则线段 $D G$ 的长为
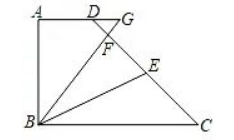
图 1 是一种推磨工具模型,图 2 是它的示意图,已知 $A B \perp P Q, A P=A Q=3 d m, A B=12 d m$, 点 $A$ 在中轴 线 $l$ 上运动, 点 $B$ 在以 $O$ 为圆心, $O B$ 长为半径的圆上运动, 且 $O B=4 d m$.
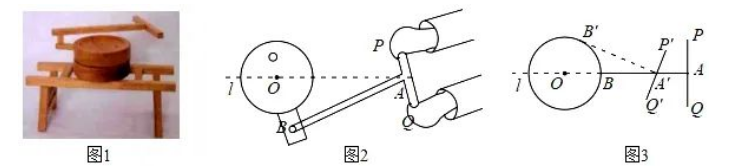
(1) 如图3, 当点 $B$ 按送时针方向运动到 $B^{\prime}$ 时, $A^{\prime} B^{\prime}$ 与 $\odot O$ 相切, 则 $A A'$
(2) 在点 $B$ 的运动过程中, 点 $P$ 与点 $O$ 之间的最短距离为
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$4 \sin 60^{\circ}-\sqrt{12}+|-3|+(\pi-2020)^{\circ}$.
解分式方程: $\frac{3}{x-2}=\frac{1}{x}$.
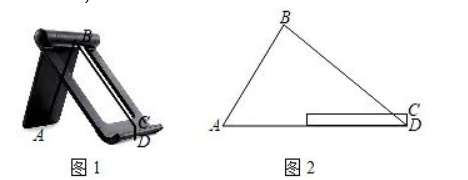
. 如图 1 是一手机支架,其中 $A B=8 \mathrm{~cm}$, 底麼 $C D=1 \mathrm{~cm}$, 当点 $A$ 正好落在桌面上时如图2所示, $\angle A B C=$ $80^{\circ}, \angle A=60^{\circ}$.
(1) 求点 $B$ 到桌面 $A D$ 的距离;
(2) 求 $B C$ 的长. (结果精确到 $0.1 \mathrm{~cm}$; 参考数据: $\sin 50^{\circ} \approx 0.77, \cos 50^{\circ} \approx 0.64, \tan 50^{\circ} \approx 1.19$, $\sqrt{3} \approx 1.73)$
某学校为了解学生疫情期间一天在线学习时长,进行了一次随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
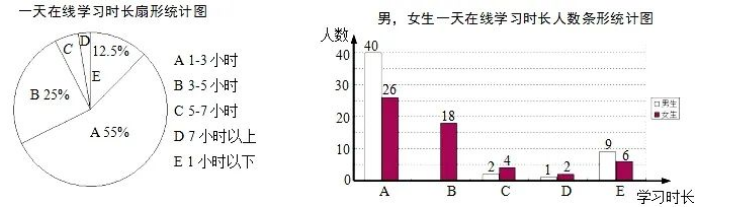
(1)求参与间卷调查的总人数.
(2) 补全条形统计图, 并求出一天在线学习“5-7个小时” 的扇形圆心角度数.
(3)若该校共有学生1800名, 试估计全校一天在线学习“7小时以上”的学生人数.
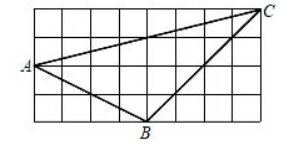
如图,在 $8 \times 4$ 的网格中,每个小正方形的边长均为 1 ,点 $A, B, C$ 都是格点 (小正方形的顶点), 完成 下列画图.
(1) 画出 $\triangle A B C$ 的重心 $P$.
(2)在已知网格中找出所有格点 $D$, 使点 $D$ 与 $\triangle A B C$ 的其中两个顶点构成的三角形的面积与 $\triangle A B C$ 的面 积相等
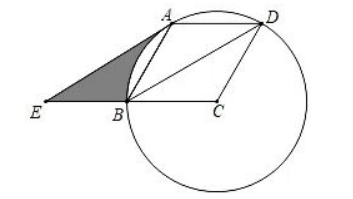
如图,已知 $\odot C$ 过菱形 $A B C D$ 的三个顶点 $B, A, D$, 连结 $B D$, 过点 $A$ 作 $A E \| B D$ 交射线 $C B$ 于点 $E$.
(1) 求证: $A E$ 是 $\odot C$ 的切线.
(2) 若半径为 2 , 求图中线段 $A E$ 、线段 $B E$ 和 $\widehat{\mathrm{AB}}$ 围成的部分的面积.
(3) 在 (2) 的条件 $F$, 在 $\odot C$ 上取点 $F$, 连结 $A F$, 使 $\angle D A F=15^{\circ}$, 求点 $F$ 到直线 $A D$ 的距离.
我们知道求函数图象的交点坐标,可以联立两个函数解析式组成方程组,方程组的解就是交点的坐 标. 如:求直线 $y=2 x+3$ 与 $y=-x+6$ 的交点坐标,我们可以联立两个解析式得到方程组 $\left\{\begin{array}{l}y=2 x+3 \\ y=-x+6\end{array}\right.$, 解得 $\left\{\begin{array}{l}\mathrm{x}=1 \\ \mathrm{y}=5\end{array}\right.$, 所以直线 $y=2 x+3$ 与 $y=-x+6$ 的交点坐标为 $(1 , 5)$. 请利用上述知识解决下列问题:
(1) 已知直线 $y=k x-2$ 和扡物线 $y=x^2-2 x+3$ ,
① 当 $k=4$ 时, 求直线与抛物线的交点坐标;
②当 $k$ 为何值时, 直线与拋物线只有一个交点?
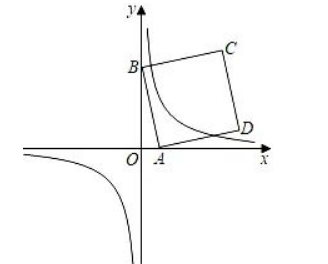
(2) 已知点 $A(a, 0)$ 是 $x$ 轴上的动点, $B(0,4 \sqrt{2})$, 以 $A B$ 为边在 $A B$ 右侧做正方形 $A B C D$, 当正方形 $2 \sqrt{2}$
$A B C D$ 的边与反比例函数 $y=\overline{\mathrm{x}}$ 的图象有 4 个交点时, 试求 $a$ 的取值范围.
如图1,矩形 $A B C D$ 中, $A B=8, B C=6$, 点 $E, F$ 分别为 $A B, A D$ 边上任意一点, 现将 $\triangle A E F$ 沿直线 $E F$ 对折,点 $A$ 对应点为点 $G$.
(1) 如图2, 当 $E F // B D$, 且点 $G$ 落在对角线 $B D$ 上时, 求 $D G$ 的长;
(2) 如图3, 连接 $D G$, 当 $E F// B D$ 且 $\triangle D F G$ 是直角三角形时, 求 $A E$ 的值;
(3) 当 $A E=2 A F$ 时, $F G$ 的延长线交 $\triangle B C D$ 的边于点 $H$, 是否存在一点 $H$, 使得以 $E, H, G$ 为顶点的三角 形与 $\triangle A E F$ 相似, 若存在, 请求出 $A E$ 的值; 若不存在, 请说明理由