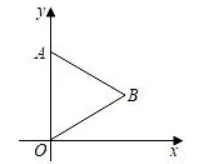
如图, 将等边 $\triangle A O B$ 放在平面直角坐标系中, 点 $A$ 的坐标为 $(0,4)$, 点 $B$ 在第一象限, 将等边 $\triangle A O B$ 绕 点 $O$ 顺时针旋堑 $180^{\circ}$ 得到 $\triangle A^{\prime} O B^{\prime}$ ,则点 $B$ 的对应点 $B^{\prime}$ 的坐标是
A
$(2 \sqrt{3}, 2)$
B
$(2 \sqrt{3},-2)$
C
$(-2 \sqrt{3},-2)$
D
$(0,-4)$
E
F